The goal of BBcor is to provide an efficient way to obtain samples from the posterior distribution of various correlation coefficients:
Pearson (method = "pearson")
Spearman (method = "spearman")
Gaussian Rank (method = "gaussian_rank")
Kendall (method = "kendall")
Blomqvist (method = "blomqvist"; median correlation)
Polychoric (method = "polychoric")
The method is based on Rubin (1981) and described in Rodriguez and Williams (2021).
You can install the development version from GitHub with:
This is a basic example which shows you how to solve a common problem, i.e., estimating correlations:
library(BBcor)
## basic example code
# data
Y <- mtcars[,1:5]
# sample posterior
bb_sample <- bbcor(Y, method = "spearman")
# correlation matrix
bb_sample$cor_mean
#> [,1] [,2] [,3] [,4] [,5]
#> [1,] 1.0000000 -0.9111911 -0.9081057 -0.8933434 0.6478409
#> [2,] -0.9111911 1.0000000 0.9284490 0.9016077 -0.6767364
#> [3,] -0.9081057 0.9284490 1.0000000 0.8501056 -0.6806186
#> [4,] -0.8933434 0.9016077 0.8501056 1.0000000 -0.5193009
#> [5,] 0.6478409 -0.6767364 -0.6806186 -0.5193009 1.0000000It is also possible to obtain partial correlations from the object bb_sample:
# convert
pcors <- cor_2_pcor(bb_sample)
# partial correlation matrix
pcors$pcor_mean
#> [,1] [,2] [,3] [,4] [,5]
#> [1,] 1.00000000 -0.09485614 -0.38536808 -0.45399594 0.1852590
#> [2,] -0.09485614 1.00000000 0.46793163 0.49707586 -0.3042260
#> [3,] -0.38536808 0.46793163 1.00000000 -0.04717437 -0.1366473
#> [4,] -0.45399594 0.49707586 -0.04717437 1.00000000 0.3524484
#> [5,] 0.18525904 -0.30422602 -0.13664735 0.35244840 1.0000000Note that the objects bb_sample and pcors include a 3D array with the sampled correlation or partial correlation matrices.
The posterior samples can be summarized as follows
post_summary <- posterior_samples(pcors, summary = TRUE, cred = 0.95)
# print
post_summary
#> Relation Post.mean Post.sd Cred.lb Cred.ub
#> 1 mpg--cyl -0.0949 0.1692 -0.4124 0.2475
#> 2 mpg--disp -0.3854 0.1569 -0.6693 -0.0585
#> 3 cyl--disp 0.4679 0.1374 0.1779 0.7034
#> 4 mpg--hp -0.4540 0.1284 -0.6771 -0.1806
#> 5 cyl--hp 0.4971 0.1205 0.2392 0.7155
#> 6 disp--hp -0.0472 0.1386 -0.3173 0.2221
#> 7 mpg--drat 0.1853 0.1810 -0.1898 0.5165
#> 8 cyl--drat -0.3042 0.1439 -0.5619 -0.0110
#> 9 disp--drat -0.1366 0.1428 -0.4123 0.1481
#> 10 hp--drat 0.3524 0.1917 -0.0608 0.6881Note that setting summary = FALSE returns the posterior samples in a data frame.
Comparisons can then be made using the compare function using a string to specify which comparisons to be made
comparisons <- c("mpg--cyl > mpg--disp",
"mpg--disp - mpg--hp = 0")
post_comparisons <- compare(comparisons,
obj = pcors,
cred = 0.9)
post_comparisons
#> bayeslincom: Linear Combinations of Posterior Samples
#> ------
#> Call:
#> lin_comb.bbcor(lin_comb = lin_comb, obj = obj, ci = ci, rope = rope,
#> contrast = contrast)
#> ------
#> Combinations:
#> C1: mpg--cyl > mpg--disp
#> C2: mpg--disp - mpg--hp = 0
#> ------
#> Posterior Summary:
#>
#> Post.mean Post.sd Cred.lb Cred.ub Pr.less Pr.greater
#> C1 0.29 0.23 -0.1 0.66 0.10 0.90
#> C2 0.07 0.23 -0.3 0.45 0.38 0.62
#> ------
#> Note:
#> Pr.less: Posterior probability less than zero
#> Pr.greater: Posterior probability greater than zero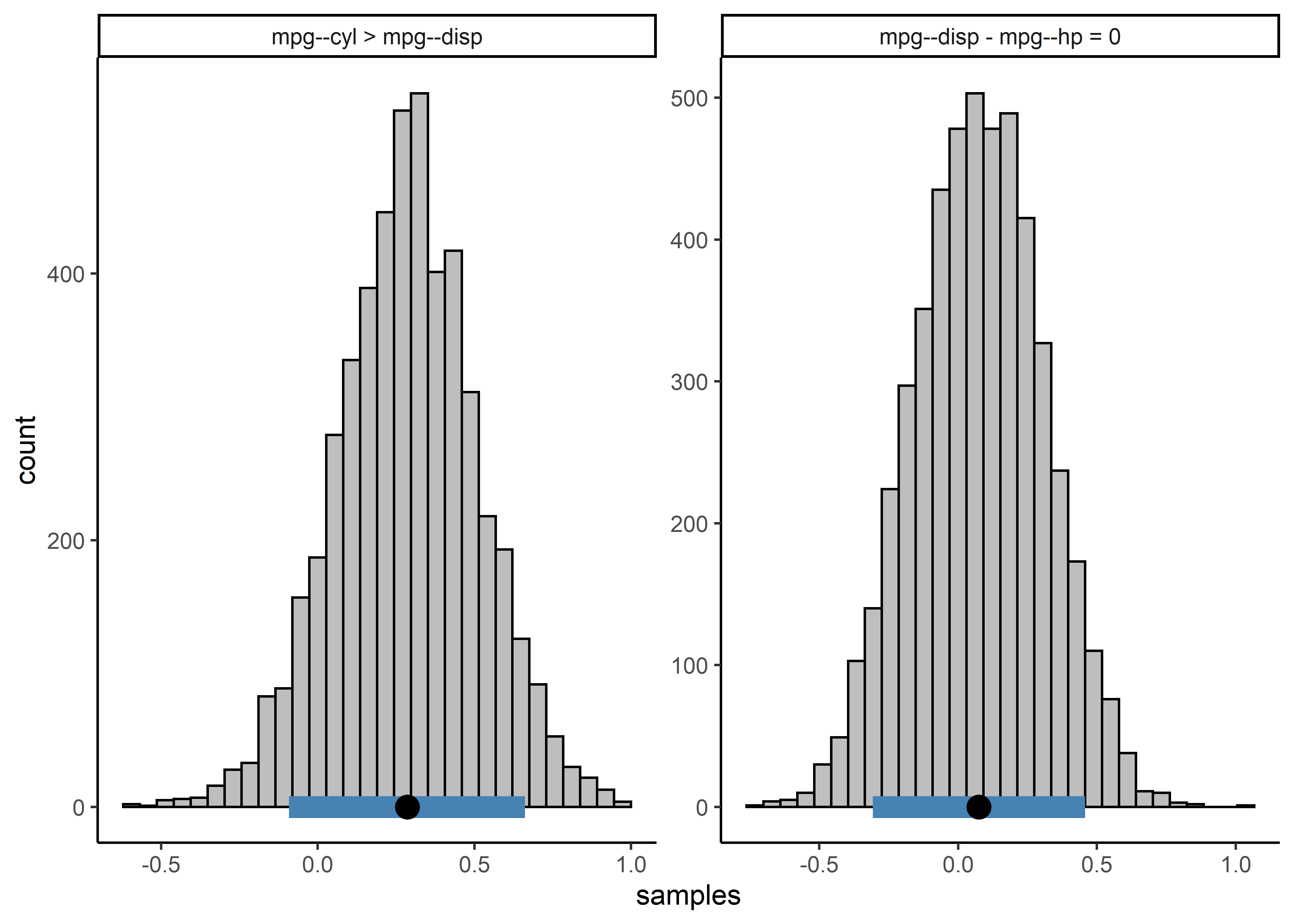
or with a contrast matrix
contrast_mat <- matrix(c(1, -1, 0,
0, 1, -1),
nrow = 2,
byrow = TRUE)
post_comparisons <- compare(c("mpg--cyl", "mpg--disp", "mpg--hp"),
obj = pcors,
contrast = contrast_mat,
cred = 0.9)
post_comparisons
#> bayeslincom: Linear Combinations of Posterior Samples
#> ------
#> Call:
#> lin_comb.bbcor(lin_comb = lin_comb, obj = obj, ci = ci, rope = rope,
#> contrast = contrast)
#> ------
#> Combinations:
#> C1: C1
#> C2: C2
#> ------
#> Posterior Summary:
#>
#> Post.mean Post.sd Cred.lb Cred.ub Pr.less Pr.greater
#> C1 0.29 0.23 -0.1 0.66 0.10 0.90
#> C2 0.07 0.23 -0.3 0.45 0.38 0.62
#> ------
#> Note:
#> Pr.less: Posterior probability less than zero
#> Pr.greater: Posterior probability greater than zeroRodriguez, Josue E, and Donald R Williams. 2021. “Painless Posterior Sampling: Bayesian Bootstrapped Correlation Coefficients.”
Rubin, Donald B. 1981. “The Bayesian Bootstrap.” The Annals of Statistics, 130–34.