


Fast Robust Moments – Pick Three!
Fast, numerically robust, higher order moments in R, computed via Rcpp, mostly as an exercise to learn Rcpp. Supports computation on vectors and matrices, and Monoidal append (and unappend) of moments. Computations are via the Welford-Terriberry algorithm, as described by Bennett et al.
– Steven E. Pav, shabbychef@gmail.com
This package can be installed from CRAN, via drat, or from github:
# via CRAN:
install.packages("fromo")
# via drat:
if (require(drat)) {
drat:::add("shabbychef")
install.packages("fromo")
}
# get snapshot from github (may be buggy)
if (require(devtools)) {
install_github("shabbychef/fromo")
}Currently the package functionality can be divided into the following: * Functions which reduce a vector to an array of moments. * Functions which take a vector to a matrix of the running moments. * Functions which transform a vector to some normalized form, like a centered, rescaled, z-scored sample, or a summarized form, like the running Sharpe or t-stat. * Functions for computing the covariance of a vector robustly. * Object representations of moments with join and unjoin methods.
A function which computes, say, the kurtosis, typically also computes the mean and standard deviation, and has performed enough computation to easily return the skew. However, the default functions in R for higher order moments discard these lower order moments. So, for example, if you wish to compute Merten’s form for the standard error of the Sharpe ratio, you have to call separate functions to compute the kurtosis, skew, standard deviation, and mean.
The summary functions in fromo return all the moments up to some order, namely the functions sd3, skew4, and kurt5. The latter of these, kurt5 returns an array of length 5 containing the excess kurtosis, the skewness, the standard deviation, the mean, and the observation count. (The number in the function name denotes the length of the output.) Along the same lines, there are summarizing functions that compute centered moments, standardized moments, and ‘raw’ cumulants:
cent_moments: return a k+1-vector of the kth centered moment, the k-1th, all the way down to the 2nd (the variance), then the mean and the observation count.std_moments: return a k+1-vector of the kth standardized moment, the k-1th, all the way down to the 3rd, then the standard deviation, the mean, and the observation count.cent_cumulants: computes the centered cumulants (yes, this is redundant, but they are not standardized). return a k+1-vector of the kth raw cumulant, the k-1th, all the way down to the second, then the mean, and the observation count.std_cumulants: computes the standardized (and, of course, centered) cumulants. return a k+1-vector of the kth standardized cumulant, all the way down to the third, then the variance, the mean, and the observation count.library(fromo)
set.seed(12345)
x <- rnorm(1000, mean = 10, sd = 2)
show(cent_moments(x, max_order = 4, na_rm = TRUE))## [1] 47.276 -0.047 3.986 10.092 1000.000## [1] 3.0e+00 -5.9e-03 2.0e+00 1.0e+01 1.0e+03## [1] -0.388 -0.047 3.986 10.092 1000.000## [1] -2.4e-02 -5.9e-03 4.0e+00 1.0e+01 1.0e+03In theory these operations should be just as fast as the default functions, but faster than calling multiple default functions. Here is a speed comparison of the basic moment computations:
library(fromo)
library(moments)
library(microbenchmark)
set.seed(123)
x <- rnorm(1000)
dumbk <- function(x) {
c(kurtosis(x) - 3, skewness(x), sd(x), mean(x),
length(x))
}
microbenchmark(kurt5(x), skew4(x), sd3(x), dumbk(x),
dumbk(x), kurtosis(x), skewness(x), sd(x), mean(x))## Error in `levels<-`(`*tmp*`, value = if (nl == nL) as.character(labels) else paste0(labels, : factor level [5] is duplicatedx <- rnorm(1e+07, mean = 1e+12)
microbenchmark(kurt5(x), skew4(x), sd3(x), dumbk(x),
kurtosis(x), skewness(x), sd(x), mean(x), times = 10L)## Unit: milliseconds
## expr min lq mean median uq max neval cld
## kurt5(x) 1408 1409 1414 1413 1418 1424 10 e
## skew4(x) 801 802 813 804 815 871 10 d
## sd3(x) 66 66 67 66 67 69 10 b
## dumbk(x) 1647 1650 1674 1655 1712 1734 10 f
## kurtosis(x) 802 804 813 806 811 869 10 d
## skewness(x) 777 780 789 781 787 822 10 c
## sd(x) 45 45 46 46 46 47 10 b
## mean(x) 16 17 17 17 17 18 10 aMany of the methods now support the computation of weighted moments. There are a few options around weights: whether to check them for negative values, whether to normalize them to unit mean.
library(fromo)
library(moments)
library(microbenchmark)
set.seed(987)
x <- rnorm(1000)
w <- runif(length(x))
# no weights:
show(cent_moments(x, max_order = 4, na_rm = TRUE))## [1] 2.9e+00 1.2e-02 1.0e+00 1.0e-02 1.0e+03## [1] 3.1e+00 4.1e-02 1.0e+00 1.3e-02 1.0e+03# if you turn off weight normalization, the last
# element is sum(wts):
show(cent_moments(x, max_order = 4, wts = w, na_rm = TRUE,
normalize_wts = FALSE))## [1] 3.072 0.041 1.001 0.013 493.941# let's compare for speed!
x <- rnorm(1e+07)
w <- runif(length(x))
slow_sd <- function(x, w) {
n0 <- length(x)
mu <- weighted.mean(x, w = w)
sg <- sqrt(sum(w * (x - mu)^2)/(n0 - 1))
c(sg, mu, n0)
}
microbenchmark(sd3(x, wts = w), slow_sd(x, w))## Unit: milliseconds
## expr min lq mean median uq max neval cld
## sd3(x, wts = w) 80 81 83 83 84 87 100 a
## slow_sd(x, w) 234 243 253 247 254 382 100 bThe as.centsums object performs the summary (centralized) moment computation, and stores the centralized sums. There is a print method that shows raw, centralized, and standardized moments of the ingested data. This object supports concatenation and unconcatenation. These should satisfy ‘monoidal homomorphism’, meaning that concatenation and taking moments commute with each other. So if you have two vectors, x1 and x2, the following should be equal: c(as.centsums(x1,4),as.centsums(x2,4)) and as.centsums(c(x1,x2),4). Moreover, the following should also be equal: as.centsums(c(x1,x2),4) %-% as.centsums(x2,4)) and as.centsums(x1,4). This is a small step of the way towards fast machine learning methods (along the lines of Mike Izbicki’s Hlearn library).
Some demo code:
set.seed(12345)
x1 <- runif(100)
x2 <- rnorm(100, mean = 1)
max_ord <- 6L
obj1 <- as.centsums(x1, max_ord)
# display:
show(obj1)## class: centsums
## raw moments: 100 0.0051 0.09 -0.00092 0.014 -0.00043 0.0027
## central moments: 0 0.09 -0.0023 0.014 -0.00079 0.0027
## std moments: 0 1 -0.086 1.8 -0.33 3.8# join them together
obj1 <- as.centsums(x1, max_ord)
obj2 <- as.centsums(x2, max_ord)
obj3 <- as.centsums(c(x1, x2), max_ord)
alt3 <- c(obj1, obj2)
# it commutes!
stopifnot(max(abs(sums(obj3) - sums(alt3))) < 1e-07)
# unjoin them, with this one weird operator:
alt2 <- obj3 %-% obj1
alt1 <- obj3 %-% obj2
stopifnot(max(abs(sums(obj2) - sums(alt2))) < 1e-07)
stopifnot(max(abs(sums(obj1) - sums(alt1))) < 1e-07)We also have ‘raw’ join and unjoin methods, not nicely wrapped:
set.seed(123)
x1 <- rnorm(1000, mean = 1)
x2 <- rnorm(1000, mean = 1)
max_ord <- 6L
rs1 <- cent_sums(x1, max_ord)
rs2 <- cent_sums(x2, max_ord)
rs3 <- cent_sums(c(x1, x2), max_ord)
rs3alt <- join_cent_sums(rs1, rs2)
stopifnot(max(abs(rs3 - rs3alt)) < 1e-07)
rs1alt <- unjoin_cent_sums(rs3, rs2)
rs2alt <- unjoin_cent_sums(rs3, rs1)
stopifnot(max(abs(rs1 - rs1alt)) < 1e-07)
stopifnot(max(abs(rs2 - rs2alt)) < 1e-07)There is also code for computing co-sums and co-moments, though as of this writing only up to order 2. Some demo code for the monoidal stuff here:
set.seed(54321)
x1 <- matrix(rnorm(100 * 4), ncol = 4)
x2 <- matrix(rnorm(100 * 4), ncol = 4)
max_ord <- 2L
obj1 <- as.centcosums(x1, max_ord, na.omit = TRUE)
# display:
show(obj1)## An object of class "centcosums"
## Slot "cosums":
## [,1] [,2] [,3] [,4] [,5]
## [1,] 100.0000 -0.093 0.045 -0.0046 0.046
## [2,] -0.0934 111.012 4.941 -16.4822 6.660
## [3,] 0.0450 4.941 71.230 0.8505 5.501
## [4,] -0.0046 -16.482 0.850 117.3456 13.738
## [5,] 0.0463 6.660 5.501 13.7379 100.781
##
## Slot "order":
## [1] 2# join them together
obj1 <- as.centcosums(x1, max_ord)
obj2 <- as.centcosums(x2, max_ord)
obj3 <- as.centcosums(rbind(x1, x2), max_ord)
alt3 <- c(obj1, obj2)
# it commutes!
stopifnot(max(abs(cosums(obj3) - cosums(alt3))) < 1e-07)
# unjoin them, with this one weird operator:
alt2 <- obj3 %-% obj1
alt1 <- obj3 %-% obj2
stopifnot(max(abs(cosums(obj2) - cosums(alt2))) < 1e-07)
stopifnot(max(abs(cosums(obj1) - cosums(alt1))) < 1e-07)Since an online algorithm is used, we can compute cumulative running moments. Moreover, we can remove observations, and thus compute moments over a fixed length lookback window. The code checks for negative even moments caused by roundoff, and restarts the computation to correct; periodic recomputation can be forced by an input parameter.
A demonstration:
library(fromo)
library(moments)
library(microbenchmark)
set.seed(1234)
x <- rnorm(20)
k5 <- running_kurt5(x, window = 10L)
colnames(k5) <- c("excess_kurtosis", "skew", "stdev",
"mean", "nobs")
k5## excess_kurtosis skew stdev mean nobs
## [1,] NaN NaN NaN -1.207 1
## [2,] NaN NaN 1.05 -0.465 2
## [3,] NaN -0.34 1.16 0.052 3
## [4,] -1.520 -0.13 1.53 -0.548 4
## [5,] -1.254 -0.50 1.39 -0.352 5
## [6,] -0.860 -0.79 1.30 -0.209 6
## [7,] -0.714 -0.70 1.19 -0.261 7
## [8,] -0.525 -0.64 1.11 -0.297 8
## [9,] -0.331 -0.58 1.04 -0.327 9
## [10,] -0.331 -0.42 1.00 -0.383 10
## [11,] 0.262 -0.65 0.95 -0.310 10
## [12,] 0.017 -0.30 0.95 -0.438 10
## [13,] 0.699 -0.61 0.79 -0.624 10
## [14,] -0.939 0.69 0.53 -0.383 10
## [15,] -0.296 0.99 0.64 -0.330 10
## [16,] 1.078 1.33 0.57 -0.391 10
## [17,] 1.069 1.32 0.57 -0.385 10
## [18,] 0.868 1.29 0.60 -0.421 10
## [19,] 0.799 1.31 0.61 -0.449 10
## [20,] 1.193 1.50 1.07 -0.118 10# trust but verify
alt5 <- sapply(seq_along(x), function(iii) {
rowi <- max(1, iii - 10 + 1)
kurtosis(x[rowi:iii]) - 3
}, simplify = TRUE)
cbind(alt5, k5[, 1])## alt5
## [1,] NaN NaN
## [2,] -2.000 NaN
## [3,] -1.500 NaN
## [4,] -1.520 -1.520
## [5,] -1.254 -1.254
## [6,] -0.860 -0.860
## [7,] -0.714 -0.714
## [8,] -0.525 -0.525
## [9,] -0.331 -0.331
## [10,] -0.331 -0.331
## [11,] 0.262 0.262
## [12,] 0.017 0.017
## [13,] 0.699 0.699
## [14,] -0.939 -0.939
## [15,] -0.296 -0.296
## [16,] 1.078 1.078
## [17,] 1.069 1.069
## [18,] 0.868 0.868
## [19,] 0.799 0.799
## [20,] 1.193 1.193If you like rolling computations, do also check out the following packages (I believe they are all on CRAN):
Of these three, it seems that RollingWindow implements the optimal algorithm of reusing computations, while the other two packages gain efficiency from parallelization and implementation in C++.
Through template magic, the same code was modified to perform running centering, scaling, z-scoring and so on:
library(fromo)
library(moments)
library(microbenchmark)
set.seed(1234)
x <- rnorm(20)
xz <- running_zscored(x, window = 10L)
# trust but verify
altz <- sapply(seq_along(x), function(iii) {
rowi <- max(1, iii - 10 + 1)
(x[iii] - mean(x[rowi:iii]))/sd(x[rowi:iii])
}, simplify = TRUE)
cbind(xz, altz)## altz
## [1,] NaN NA
## [2,] 0.71 0.71
## [3,] 0.89 0.89
## [4,] -1.18 -1.18
## [5,] 0.56 0.56
## [6,] 0.55 0.55
## [7,] -0.26 -0.26
## [8,] -0.23 -0.23
## [9,] -0.23 -0.23
## [10,] -0.51 -0.51
## [11,] -0.17 -0.17
## [12,] -0.59 -0.59
## [13,] -0.19 -0.19
## [14,] 0.84 0.84
## [15,] 2.02 2.02
## [16,] 0.49 0.49
## [17,] -0.22 -0.22
## [18,] -0.82 -0.82
## [19,] -0.64 -0.64
## [20,] 2.37 2.37A list of the available running functions:
running_centered : from the current value, subtract the mean over the trailing window.running_scaled: divide the current value by the standard deviation over the trailing window.running_zscored: from the current value, subtract the mean then divide by the standard deviation over the trailing window.running_sharpe: divide the mean by the standard deviation over the trailing window. There is a boolean flag to also compute and return the Mertens’ form of the standard error of the Sharpe ratio over the trailing window in the second column.running_tstat: compute the t-stat over the trailing window.running_cumulants: computes cumulants over the trailing window.running_apx_quantiles: computes approximate quantiles over the trailing window based on the cumulants and the Cornish-Fisher approximation.running_apx_median: uses running_apx_quantiles to give the approximate median over the trailing window.The functions running_centered, running_scaled and running_zscored take an optional lookahead parameter that allows you to peek ahead (or behind if negative) to the computed moments for comparing against the current value. These are not supported for running_sharpe or running_tstat because they do not have an idea of the ‘current value’.
Here is an example of using the lookahead to z-score some data, compared to a purely time-safe lookback. Around a timestamp of 1000, you can see the difference in outcomes from the two methods:
set.seed(1235)
z <- rnorm(1500, mean = 0, sd = 0.09)
x <- exp(cumsum(z)) - 1
xz_look <- running_zscored(x, window = 301, lookahead = 150)
xz_safe <- running_zscored(x, window = 301, lookahead = 0)
df <- data.frame(timestamp = seq_along(x), raw = x,
lookahead = xz_look, lookback = xz_safe)
library(tidyr)
gdf <- gather(df, key = "smoothing", value = "x", -timestamp)
library(ggplot2)
ph <- ggplot(gdf, aes(x = timestamp, y = x, group = smoothing,
colour = smoothing)) + geom_line()
print(ph)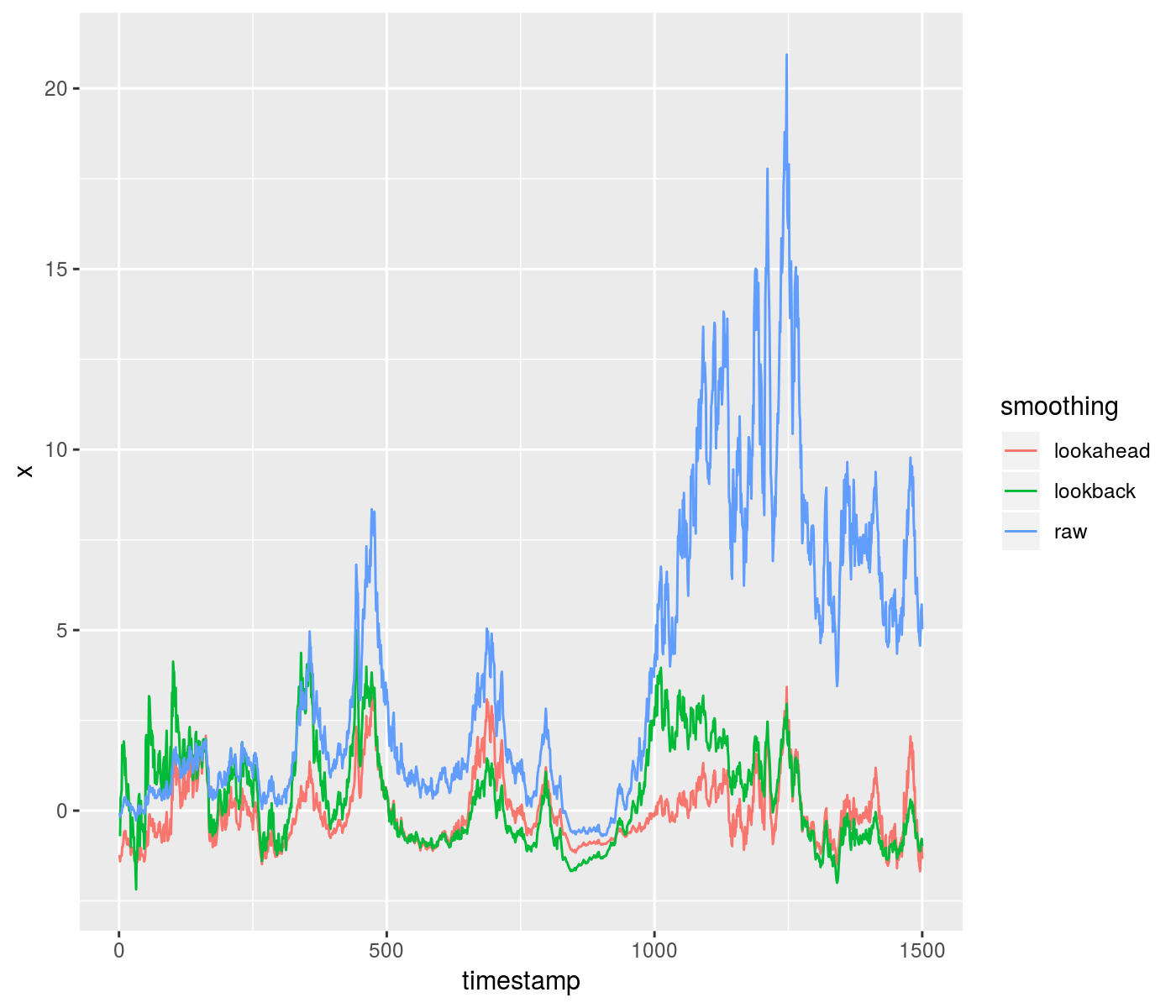
The standard running moments computations listed above work on a running window of a fixed number of observations. However, sometimes one needs to compute running moments over a different kind of window. The most common form of this is over time-based windows. For example, the following computations:
These are now supported in fromo via the t_running class of functions, which are like the running functions, but accept also the ‘times’ at which the input are marked, and optionally also the times at which one will ‘look back’ to perform the computations. The times can be computed implicitly as the cumulative sum of given (non-negative) time deltas.
Here is an example of computing the volatility of daily ‘returns’ of the Fama French Market factor, based on a one year window, computed at month ends:
# devtools::install_github('shabbychef/aqfb_data')
library(aqfb.data)
library(fromo)
# daily 'returns' of Fama French 4 factors
data(dff4)
# compute month end dates:
library(lubridate)
mo_ends <- unique(lubridate::ceiling_date(index(dff4),
"month") %m-% days(1))
res <- t_running_sd3(dff4$Mkt, time = index(dff4),
window = 365.25, min_df = 180, lb_time = mo_ends)
df <- cbind(data.frame(mo_ends), data.frame(res))
colnames(df) <- c("date", "sd", "mean", "num_days")
knitr::kable(tail(df), row.names = FALSE)| date | sd | mean | num_days |
|---|---|---|---|
| 2016-07-31 | 1.09 | 0.02 | 251 |
| 2016-08-31 | 0.98 | 0.05 | 253 |
| 2016-09-30 | 0.94 | 0.06 | 253 |
| 2016-10-31 | 0.91 | 0.02 | 252 |
| 2016-11-30 | 0.91 | 0.04 | 253 |
| 2016-12-31 | 0.86 | 0.05 | 252 |
And the plot of the time series:
library(ggplot2)
library(scales)
ph <- df %>% ggplot(aes(date, 0.01 * sd)) + geom_line() +
geom_point(alpha = 0.1) + scale_y_continuous(labels = scales::percent) +
labs(x = "lookback date", y = "standard deviation of percent returns",
title = "rolling 1 year volatility of daily Mkt factor returns, computed monthly")
print(ph)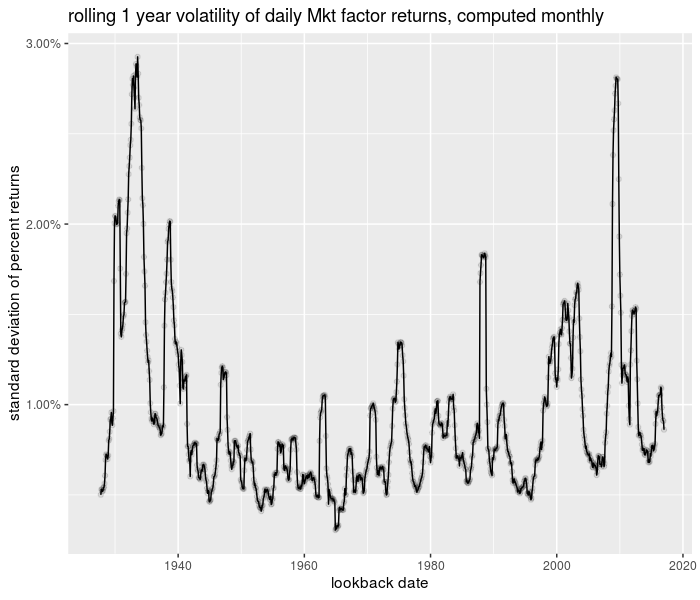
We make every attempt to balance numerical robustness, computational efficiency and memory usage. As a bit of strawman-bashing, here we microbenchmark the running Z-score computation against the naive algorithm:
library(fromo)
library(moments)
library(microbenchmark)
set.seed(4422)
x <- rnorm(10000)
dumb_zscore <- function(x, window) {
altz <- sapply(seq_along(x), function(iii) {
rowi <- max(1, iii - window + 1)
xrang <- x[rowi:iii]
(x[iii] - mean(xrang))/sd(xrang)
}, simplify = TRUE)
}
val1 <- running_zscored(x, 250)
val2 <- dumb_zscore(x, 250)
stopifnot(max(abs(val1 - val2), na.rm = TRUE) <= 1e-14)
microbenchmark(running_zscored(x, 250), dumb_zscore(x,
250))## Unit: microseconds
## expr min lq mean median uq max neval cld
## running_zscored(x, 250) 314 330 352 343 362 449 100 a
## dumb_zscore(x, 250) 215985 228979 244549 240660 257504 345485 100 bMore seriously, here we compare the running_sd3 function, which computes the standard deviation, mean and number of elements with the roll_sd and roll_mean functions from the roll package.
# dare I?
library(fromo)
library(microbenchmark)
library(roll)
set.seed(4422)
x <- rnorm(1e+05)
xm <- matrix(x)
v1 <- running_sd3(xm, 250)
rsd <- roll::roll_sd(xm, 250)
rmu <- roll::roll_mean(xm, 250)
# compute error on the 1000th row:
stopifnot(max(abs(v1[1000, ] - c(rsd[1000], rmu[1000],
250))) < 1e-14)
# now timings:
microbenchmark(running_sd3(xm, 250), roll::roll_mean(xm,
250), roll::roll_sd(xm, 250))## Unit: microseconds
## expr min lq mean median uq max neval cld
## running_sd3(xm, 250) 2990 3007 3246 3322 3408 4335 100 b
## roll::roll_mean(xm, 250) 731 739 849 883 911 1382 100 a
## roll::roll_sd(xm, 250) 3452 3641 3764 3778 3814 5187 100 cOK, that’s not a fair comparison: roll_mean is optimized to work columwise on a matrix. Let’s unbash this strawman. I create a function using fromo::running_sd3 to compute a running mean or running standard deviation columnwise on a matrix, then compare that to roll_mean and roll_sd:
library(fromo)
library(microbenchmark)
library(roll)
set.seed(4422)
xm <- matrix(rnorm(2e+05), ncol = 100)
fromo_sd <- function(x, wins) {
apply(x, 2, function(xc) {
running_sd3(xc, wins)[, 1]
})
}
fromo_mu <- function(x, wins) {
apply(x, 2, function(xc) {
running_sd3(xc, wins)[, 2]
})
}
wins <- 500
v1 <- fromo_sd(xm, wins)
rsd <- roll::roll_sd(xm, wins, min_obs = 3)
v2 <- fromo_mu(xm, wins)
rmu <- roll::roll_mean(xm, wins)
# compute error on the 1000th row:
stopifnot(max(abs(v1[1000, ] - rsd[1000, ])) < 1e-14)
stopifnot(max(abs(v2[1000, ] - rmu[1000, ])) < 1e-14)
# now timings: note fromo_mu and fromo_sd do
# exactly the same work, so only time one of them
microbenchmark(fromo_sd(xm, wins), roll::roll_mean(xm,
wins), roll::roll_mean(xm, wins, parallel_for = "cols"),
roll::roll_mean(xm, wins, parallel_for = "rows"),
roll::roll_sd(xm, wins), times = 50L)## Error in roll::roll_mean(xm, wins, parallel_for = "cols"): unused argument (parallel_for = "cols")This was somewhat unexpected. I did not think the fromo functions would be faster than roll_sd, much less roll_mean. From these benchmarks, I suspected that my computer was not taking advantage of parallelization, since the different calls to roll_mean had the same timings. To check, I timed roll_mean for the same data size, but for larger rolling windows. During the following timing, I confirmed that all eight cores on my laptop were at 100% utilization. I believe the problem is that roll_mean is literally recomputing the moments over the entire window for every cell of the output, instead of reusing computations, which fromo mostly does:
library(roll)
library(microbenchmark)
set.seed(91823)
xm <- matrix(rnorm(2e+05), ncol = 10)
fromo_mu <- function(x, wins, ...) {
apply(x, 2, function(xc) {
running_sd3(xc, wins, ...)[, 2]
})
}
microbenchmark(roll::roll_mean(xm, 10, min_obs = 3),
roll::roll_mean(xm, 100, min_obs = 3), roll::roll_mean(xm,
1000, min_obs = 3), roll::roll_mean(xm, 10000,
min_obs = 3), fromo_mu(xm, 10, min_df = 3),
fromo_mu(xm, 100, min_df = 3), fromo_mu(xm, 1000,
min_df = 3), fromo_mu(xm, 10000, min_df = 3),
times = 100L)## Unit: microseconds
## expr min lq mean median uq max neval cld
## roll::roll_mean(xm, 10, min_obs = 3) 630 731 842 786 831 5080 100 a
## roll::roll_mean(xm, 100, min_obs = 3) 645 731 809 786 835 2352 100 a
## roll::roll_mean(xm, 1000, min_obs = 3) 642 723 791 765 814 2548 100 a
## roll::roll_mean(xm, 10000, min_obs = 3) 619 718 810 760 818 2493 100 a
## fromo_mu(xm, 10, min_df = 3) 5707 5898 6201 6097 6330 8060 100 b
## fromo_mu(xm, 100, min_df = 3) 6888 7063 7485 7395 7648 9460 100 c
## fromo_mu(xm, 1000, min_df = 3) 17937 18193 19319 18981 19947 23671 100 d
## fromo_mu(xm, 10000, min_df = 3) 70518 71236 73727 72855 74553 92000 100 eThe runtime for operations from roll grow with the window size. The equivalent operations from fromo appear to also consume more time. In theory they would be invariant with respect to window size, but I coded them to ‘restart’ the computation periodically for improved accuracy. The user has control over how often this happens, in order to balance speed and accuracy. Here I set that parameter very large to show that runtimes need not grow with window size:
library(fromo)
library(microbenchmark)
set.seed(91823)
xm <- matrix(rnorm(2e+05), ncol = 10)
fromo_mu <- function(x, wins, ...) {
apply(x, 2, function(xc) {
running_sd3(xc, wins, ...)[, 2]
})
}
rp <- 1L + nrow(xm)
microbenchmark(fromo_mu(xm, 10, min_df = 3, restart_period = rp),
fromo_mu(xm, 100, min_df = 3, restart_period = rp),
fromo_mu(xm, 1000, min_df = 3, restart_period = rp),
fromo_mu(xm, 10000, min_df = 3, restart_period = rp),
times = 100L)## Unit: milliseconds
## expr min lq mean median uq max neval cld
## fromo_mu(xm, 10, min_df = 3, restart_period = rp) 6.1 6.5 6.8 6.5 6.8 9.7 100 a
## fromo_mu(xm, 100, min_df = 3, restart_period = rp) 6.2 6.5 6.8 6.5 6.7 10.6 100 a
## fromo_mu(xm, 1000, min_df = 3, restart_period = rp) 6.2 6.5 6.9 6.6 6.8 9.7 100 a
## fromo_mu(xm, 10000, min_df = 3, restart_period = rp) 6.5 6.6 7.0 6.7 7.0 10.4 100 aHere are some more benchmarks, also against the rollingWindow package, for running sums:
library(microbenchmark)
library(fromo)
library(RollingWindow)
library(roll)
set.seed(12345)
x <- rnorm(10000)
xm <- matrix(x)
wins <- 1000
# run fun on each wins sized window...
silly_fun <- function(x, wins, fun, ...) {
xout <- rep(NA, length(x))
for (iii in seq_along(x)) {
xout[iii] <- fun(x[max(1, iii - wins + 1):iii],
...)
}
xout
}
vals <- list(running_sum(x, wins, na_rm = FALSE), RollingWindow::RollingSum(x,
wins, na_method = "ignore"), roll::roll_sum(xm,
wins), silly_fun(x, wins, sum, na.rm = FALSE))
# check all equal?
stopifnot(max(unlist(lapply(vals[2:length(vals)], function(av) {
err <- vals[[1]] - av
max(abs(err[wins:length(err)]), na.rm = TRUE)
}))) < 1e-12)
# benchmark it
microbenchmark(running_sum(x, wins, na_rm = FALSE),
RollingWindow::RollingSum(x, wins), running_sum(x,
wins, na_rm = TRUE), RollingWindow::RollingSum(x,
wins, na_method = "ignore"), roll::roll_sum(xm,
wins))## Unit: microseconds
## expr min lq mean median uq max neval cld
## running_sum(x, wins, na_rm = FALSE) 67 72 74 73 75 84 100 a
## RollingWindow::RollingSum(x, wins) 104 108 110 110 111 134 100 d
## running_sum(x, wins, na_rm = TRUE) 97 103 106 105 107 174 100 c
## RollingWindow::RollingSum(x, wins, na_method = "ignore") 268 278 282 281 286 306 100 e
## roll::roll_sum(xm, wins) 92 95 98 96 99 155 100 bAnd running means:
library(microbenchmark)
library(fromo)
library(RollingWindow)
library(roll)
set.seed(12345)
x <- rnorm(10000)
xm <- matrix(x)
wins <- 1000
vals <- list(running_mean(x, wins, na_rm = FALSE),
RollingWindow::RollingMean(x, wins, na_method = "ignore"),
roll::roll_mean(xm, wins), silly_fun(x, wins, mean,
na.rm = FALSE))
# check all equal?
stopifnot(max(unlist(lapply(vals[2:length(vals)], function(av) {
err <- vals[[1]] - av
max(abs(err[wins:length(err)]), na.rm = TRUE)
}))) < 1e-12)
# benchmark it:
microbenchmark(running_mean(x, wins, na_rm = FALSE,
restart_period = 1e+05), RollingWindow::RollingMean(x,
wins), running_mean(x, wins, na_rm = TRUE, restart_period = 1e+05),
RollingWindow::RollingMean(x, wins, na_method = "ignore"),
roll::roll_mean(xm, wins))## Unit: microseconds
## expr min lq mean median uq max neval cld
## running_mean(x, wins, na_rm = FALSE, restart_period = 1e+05) 66 71 74 74 75 102 100 a
## RollingWindow::RollingMean(x, wins) 129 135 138 138 139 185 100 d
## running_mean(x, wins, na_rm = TRUE, restart_period = 1e+05) 95 102 105 105 106 138 100 b
## RollingWindow::RollingMean(x, wins, na_method = "ignore") 288 302 308 309 313 348 100 e
## roll::roll_mean(xm, wins) 103 109 112 111 113 165 100 c