This package implements the interval-valued kriging models described in Bean et. al. (2019a). Details regarding the algorithmic implementation can be found in Bean et. al. (2019b).
The package can be most conveniently installed using the command
For the most up to date version, please use the command
Note that the github installation makes use of the devtools package (Wickham, Hester, and Chang 2019). The most current version of this package can be found at .
The package revolves around its main function named intkrige. Information about this function can be obtained by entering
in the console.
The package also contains an interval-valued design ground snow load dataset named utsnow and an interval-valued temperature dataset named ohtemp. These data are available by installing the intkrige package and invoking the command
with dataset documentation obtained by
Once installed, this package runs simple and ordinary interval-valued kriging models. The following example comes from the design ground snow load application described in Bean et. al. (Bean, Sun, and Maguire 2019a). The snow load problem requires a proper consideration of the effect of elevation on ground snow loads prior to input into kriging. The current interval-valued kriging models allow for linear considerations of secondary variables in the model predictions. Such models are akin to “kriging with an external drift” (Goovaerts 1997) or “simple kriging with varying local means” (Goovaerts 2000).
The example shows how to make an interval valued kriging design ground snow load prediction (after removing the effect of elevation) for Logan, Utah. Many of the functions in the following examples are wrappers to functions in the gstat and sp packages (Pebesma 2004; Gräler, Pebesma, and Heuvelink 2016; Bivand et al. 2013) designed to make the interval-valued spatial analysis more convenient. Additional details are provided in the vignette associated with this package. This vignette can be accessed with the command
The intkrige package relies on interval-valued spatial objects. These objects are named intsp and intgrd respectively. intsp inherits directly from SpatialPointsDataFrame objects in the sp class, while intgrd inherits from SpatialPixelsDataFrame. These class extensions are created using the interval() function as demonstrated below.
library(intkrige)
#> Loading required package: sp
#> Loading required package: gstat
#> Registered S3 method overwritten by 'xts':
#> method from
#> as.zoo.xts zoo
#> Loading required package: raster
# First, define the location and elevation of interest.
# (In this case we pick coordinates of Utah State University)
templocs <- data.frame(lat = 41.745, long = -111.810, ELEVATION = 1456)
sp::coordinates(templocs) <- c("long", "lat")
sp::proj4string(templocs) <- "+proj=longlat +ellps=WGS84
+datum=WGS84 +no_defs +towgs84=0,0,0"
# Load the Utah Snow Load Data
data(utsnow)
utsnow.sp <- utsnow
# Convert to an 'intsp' object that inherits a SpatialPointsDataFrame
sp::coordinates(utsnow.sp) <- c("LONGITUDE", "LATITUDE")
sp::proj4string(utsnow.sp) <- sp::proj4string(templocs)
interval(utsnow.sp) <- c("minDL", "maxDL")The objects are defined by the interval slot. Intervals must be defined according to their upper and lower endpoints. The program will not accept values in the interval slot that do not meet this criteria. The interval-valued kriging models in the package rely on characterizations of intervals by their center and radius. The center/radius values are calculated automatically as needed by the various functions. The rationale is behind this approach is that intervals are easier to read using lower/upper endpoint convention, but easier to visualize and analyze using center/radius convention. One consequence of this approach is that variable transformations are most conveniently performed using the lower/upper endpoint characterization.
Next, we demonstrate how to create and fit empirical variograms. The functions that accomplish this task are fairly shallow wrappers to the functions in the gstat package. These function in the intkrige package simplify the workflow by fitting the center, radius, and center/radius variograms using the information contained in the interval slot. The intvariogram function defines the empirical variograms, while the fit.intvariogram function automatically fits variograms to the output of intvariogram. Note that intvariogram defines an intvariogram class which is the only class that fit.intvariogram will accept. This new class designation is intended to ensure that intvariogram and fit.intvariogram are always used in tandem. These particular variograms first account for the effect of elevation on ground snow loads before calculating the empirical variograms.
# Define the formulas we will use to define the intervals.
temp_formulas <- list(center ~ ELEVATION,
radius*(ELEVATION/median(ELEVATION)) ~ 1)
# Define, fit and check the variogram fits.
varios <- intvariogram(utsnow.sp,
formulas = temp_formulas)
varioFit <- fit.intvariogram(varios, models = gstat::vgm(c("Sph", "Sph", "Gau")))
intvCheck(varios, varioFit)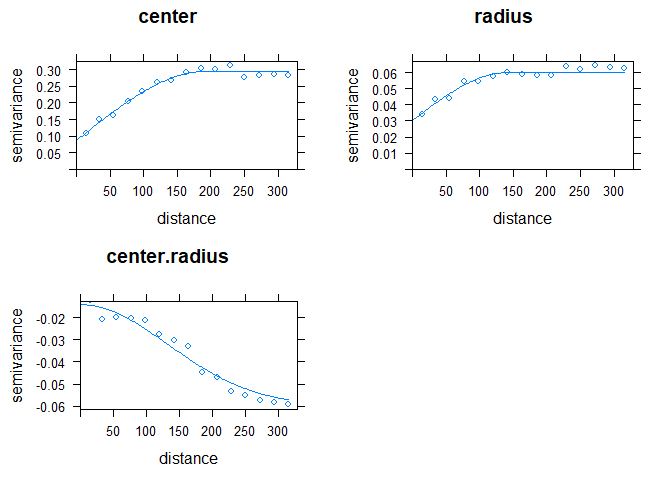
With variograms defined for each component of the interval, we are now ready to make interval-valued predictions using our interval-valued kriging models. If you explore the function documentation, you will notice that many of the function arguments relate to the Newton-Raphson optimization technique that is used to calculate the kriging model weights. These arguments should not need to be changed from the defaults for most user purposes. The following demonstrates an ordinary kriging model after accounting for elevation.
preds <- intkrige::intkrige(locations = utsnow.sp,
newdata = templocs,
models = varioFit,
formulas = temp_formulas)
# The final results are predicted intervals after removing the effect of elevation.
preds
#> coordinates interval ELEVATION center radius
#> 1 (-111.81, 41.745) [-0.03611231, 0.9702524] 1456 0.433943 0.5031823
#> kriging_variance warn
#> 1 0.1517327 0The interval prediction (including the elevation effect) is included in the interval slot. The raw predictions are appended to the data frame under the following variable names:
-center: the value of the interval centers returned directly from the kriging model,
-radius: raw radii predictions,
-variance: the kriging variance according the generalized L2 distance,
-warn: a boolean that is 0 for a convergent optimization and 1 for a non-convergent optimization. This quiet approach to warnings ensures a non-disruptive experience for the user when predicting a large number of locations.
Bean, Brennan, Yan Sun, and Marc Maguire. 2019a. “Interval-Valued Kriging Models for Geostatistical Mapping with Uncertain Inputs.”
———. 2019b. “Supplement to ‘Interval-Valued Kriging Models for Geostatistical Mapping with Uncertain Inputs’.”
Bivand, Roger S, Edzer J Pebesma, Virgilio Gomez-Rubio, and Edzer Jan Pebesma. 2013. Applied Spatial Data Analysis with R. 2nd ed. Vol. 747248717. Springer.
Goovaerts, Pierre. 1997. Geostatistics for Natural Resources Evaluation. Oxford University Press.
———. 2000. “Geostatistical Approaches for Incorporating Elevation into the Spatial Interpolation of Rainfall.” Journal of Hydrology 228 (1): 113–29.
Gräler, Benedikt, Edzer Pebesma, and Gerard Heuvelink. 2016. “Spatio-Temporal Interpolation Using Gstat.” The R Journal 8 (1): 204–18. https://journal.r-project.org/archive/2016-1/na-pebesma-heuvelink.pdf.
Pebesma, Edzer J. 2004. “Multivariable Geostatistics in S: The Gstat Package.” Computers & Geosciences 30: 683–91.
Wickham, Hadley, Jim Hester, and Winston Chang. 2019. Devtools: Tools to Make Developing R Packages Easier. https://github.com/r-lib/devtools.