This package provides methods to estimate models of the form
where is simple distribution, we observe periods, and , , , and are known. What is multivariate is (though, can also be multivariate) and this package is written to scale well in the cardinality of . The package uses independent particle filters as suggested by Lin et al. (2005). This particular type of filter can be used in the method suggested by Poyiadjis, Doucet, and Singh (2011). I will show an example of how to use the package through the rest of the document and highlight some implementation details.
The package can be installed from Github e.g., by calling
or from CRAN by calling
We simulate data as follows.
# simulate path of state variables
set.seed(78727269)
n_periods <- 312L
(F. <- matrix(c(.5, .1, 0, .8), 2L))## [,1] [,2]
## [1,] 0.5 0.0
## [2,] 0.1 0.8## [,1] [,2]
## [1,] 0.25 0.10
## [2,] 0.10 0.49## [,1] [,2]
## [1,] 0.333 0.194
## [2,] 0.194 1.460betas <- cbind(crossprod(chol(Q_0), rnorm(2L) ),
crossprod(chol(Q ), matrix(rnorm((n_periods - 1L) * 2), 2)))
betas <- t(betas)
for(i in 2:nrow(betas))
betas[i, ] <- betas[i, ] + F. %*% betas[i - 1L, ]
par(mar = c(5, 4, 1, 1))
matplot(betas, lty = 1, type = "l")
# simulate observations
cfix <- c(-1, .2, .5, -1) # gamma
n_obs <- 100L
dat <- lapply(1:n_obs, function(id){
x <- runif(n_periods, -1, 1)
X <- cbind(X1 = x, X2 = runif(1, -1, 1))
z <- runif(n_periods, -1, 1)
eta <- drop(cbind(1, X, z) %*% cfix + rowSums(cbind(1, z) * betas))
y <- rpois(n_periods, lambda = exp(eta))
# randomly drop some
keep <- .2 > runif(n_periods)
data.frame(y = y, X, Z = z, id = id, time_idx = 1:n_periods)[keep, ]
})
dat <- do.call(rbind, dat)
# show some properties
nrow(dat)## [1] 6242## y X1 X2 Z id time_idx
## 2 0 0.5685 0.9272 0.9845 1 2
## 3 0 -0.2260 0.9272 0.1585 1 3
## 4 1 -0.7234 0.9272 0.4847 1 4
## 5 1 -0.3010 0.9272 -0.6352 1 5
## 8 2 -0.4437 0.9272 0.8311 1 8
## 13 1 0.2834 0.9272 0.7135 1 13##
## 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
## 3881 1479 486 180 83 54 32 8 7 6 6 2 3 3 2
## 15 16 17 20 21 24 26 28
## 2 1 1 2 1 1 1 1# quick smooth of number of events vs. time
par(mar = c(5, 4, 1, 1))
plot(smooth.spline(dat$time_idx, dat$y), type = "l", xlab = "Time",
ylab = "Number of events")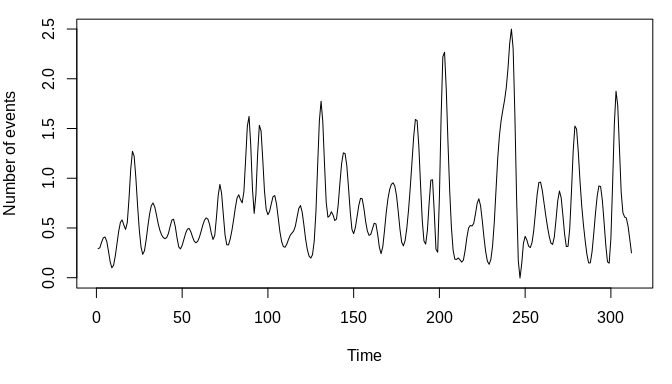
# and split by those with `Z` above and below 0
with(dat, {
z_large <- ifelse(Z > 0, "large", "small")
smooths <- lapply(split(cbind(dat, z_large), z_large), function(x){
plot(smooth.spline(x$time_idx, x$y), type = "l", xlab = "Time",
ylab = paste("Number of events -", unique(x$z_large)))
})
})

In the above, we simulate 312 (n_periods) with 100 (n_obs) individuals. Each individual has a fixed covariate, X2, and two time-varying covariates, X1 and Z. One of the time-varying covariates, Z, has a random slope. Further, the intercept is also random.
We start by estimating a generalized linear model without random effects.
##
## Call:
## glm(formula = y ~ X1 + X2 + Z, family = poisson(), data = dat)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.266 -1.088 -0.767 0.395 10.913
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -0.5558 0.0180 -30.82 < 2e-16 ***
## X1 0.2024 0.0265 7.62 2.4e-14 ***
## X2 0.5160 0.0275 18.78 < 2e-16 ***
## Z -0.9122 0.0286 -31.90 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for poisson family taken to be 1)
##
## Null deviance: 10989.1 on 6241 degrees of freedom
## Residual deviance: 9427.1 on 6238 degrees of freedom
## AIC: 14977
##
## Number of Fisher Scoring iterations: 6## 'log Lik.' -7485 (df=4)Next, we make a log-likelihood approximation with the implemented particle at the true parameters with the mssm function.
library(mssm)
ll_func <- mssm(
fixed = y ~ X1 + X2 + Z, family = poisson(), data = dat,
# make it explict that there is an intercept (not needed)
random = ~ 1 + Z, ti = time_idx, control = mssm_control(
n_threads = 5L, N_part = 500L, what = "log_density"))
system.time(
mssm_obj <- ll_func$pf_filter(
cfix = cfix, disp = numeric(), F. = F., Q = Q))## user system elapsed
## 2.047 0.011 0.527## 'log Lik.' -5865 (df=11)##
## Call: mssm(fixed = y ~ X1 + X2 + Z, family = poisson(), data = dat,
## random = ~1 + Z, ti = time_idx, control = mssm_control(n_threads = 5L,
## N_part = 500L, what = "log_density"))
##
## Family is 'poisson' with link 'log'.
## State vector is assumed to be X_t ~ N(F * X_(t-1), Q).
##
## F is
## (Intercept) Z
## (Intercept) 0.5 0.0
## Z 0.1 0.8
##
## Q's standard deviations are
## (Intercept) Z
## 0.5 0.7
##
## Q's correlation matrix is (lower triangle is shown)
## (Intercept)
## Z 0.286
##
## Fixed coefficients are
## (Intercept) X1 X2 Z
## -1.0 0.2 0.5 -1.0
##
## Log-likelihood approximation is -5865
## 500 particles are used and summary statistics for effective sample sizes are
## Mean 458.4
## sd 22.1
## Min 325.7
## Max 484.8
##
## Number of parameters 11
## Number of observations 6242We get a much larger log-likelihood as expected. We can plot the predicted values of state variables from the filter distribution.
# get predicted mean and prediction interval
filter_means <- plot(mssm_obj, do_plot = FALSE)
# plot with which also contains the true paths
for(i in 1:ncol(betas)){
be <- betas[, i]
me <- filter_means$means[i, ]
lb <- filter_means$lbs[i, ]
ub <- filter_means$ubs[i, ]
# dashed: true paths
# continuous: predicted mean from filter distribution
# dotted: prediction interval
par(mar = c(5, 4, 1, 1))
matplot(cbind(be, me, lb, ub), lty = c(2, 1, 3, 3), type = "l",
col = "black", ylab = rownames(filter_means$lbs)[i])
}

We can also get predicted values from the smoothing distribution.
# get smoothing weights
mssm_obj <- ll_func$smoother(mssm_obj)
# get predicted mean and prediction interval from smoothing distribution
smooth_means <- plot(mssm_obj, do_plot = FALSE, which_weights = "smooth")
for(i in 1:ncol(betas)){
be <- betas[, i]
me <- filter_means$means[i, ]
lb <- filter_means$lbs[i, ]
ub <- filter_means$ubs[i, ]
mes <- smooth_means$means[i, ]
lbs <- smooth_means$lbs[i, ]
ubs <- smooth_means$ubs[i, ]
# dashed: true paths
# continuous: predicted mean from filter distribution
# dotted: prediction interval
#
# smooth predictions are in a different color
par(mar = c(5, 4, 1, 1))
matplot(cbind(be, me, lb, ub, mes, lbs, ubs),
lty = c(2, 1, 3, 3, 1, 3, 3), type = "l",
col = c(rep(1, 4), rep(2, 3)), ylab = rownames(filter_means$lbs)[i])
}

# compare mean square error of the two means
rbind(filter = colMeans((t(filter_means$means) - betas)^2),
smooth = colMeans((t(smooth_means$means) - betas)^2))## (Intercept) Z
## filter 0.1035 0.2127
## smooth 0.1012 0.1906We can get the effective sample size at each point in time with the get_ess function.
## Effective sample sizes
## Mean 458.4
## sd 22.1
## Min 325.7
## Max 484.8
We can compare this what we get by using a so-called bootstrap (like) filter instead.
local({
ll_boot <- mssm(
fixed = y ~ X1 + X2 + Z, family = poisson(), data = dat,
random = ~ Z, ti = time_idx, control = mssm_control(
n_threads = 5L, N_part = 500L, what = "log_density",
which_sampler = "bootstrap"))
print(system.time(
boot_fit <- ll_boot$pf_filter(
cfix = coef(glm_fit), disp = numeric(), F. = F., Q = Q)))
plot(get_ess(boot_fit))
})## user system elapsed
## 1.929 0.012 0.504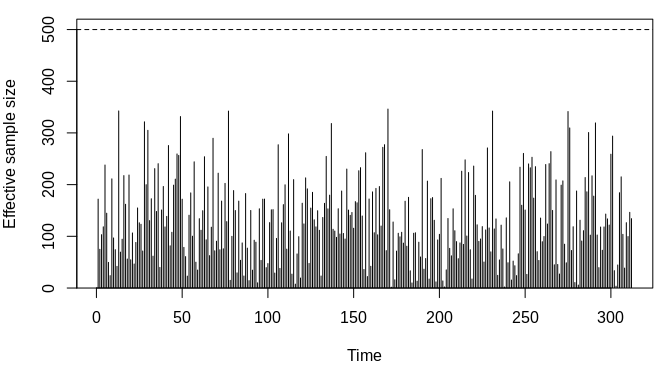
The above is not much faster (and maybe slower in this run) as the bulk of the computation is not in the sampling step. We can also compare the log-likelihood approximation with what we get if we choose parameters close to the GLM estimates.
mssm_glm <- ll_func$pf_filter(
cfix = coef(glm_fit), disp = numeric(), F. = diag(1e-8, 2),
Q = diag(1e-4^2, 2))
logLik(mssm_glm)## 'log Lik.' -7485 (df=11)One way to reduce the variance of the Monte Carlo estimate is to use antithetic variables. Two types of antithetic variables are implemented as in Durbin and Koopman (1997). That is, one balanced for location and two balanced for scale. This is currently only implemented with a t-distribution as the proposal distribution.
We start by giving some details on the locations balanced variable. Suppose we use a t-distribution with degrees of freedom, a dimensional mean of and a scale matrix . We can then generate a sample by setting
Then the location balanced variable is
For the scaled balanced variables we use that
We then define the cumulative distribution function
and set
Then the two scaled balanced variables are
We will illustrate the reduction in variance of the log-likelihood estimate. To do so, we run the particle filter with and without antithetic variables multiple times below to get an estimate of the error of the approximation.
set.seed(12769550)
compare_anti <- local({
ll_func_no_anti <- mssm(
fixed = y ~ X1 + X2 + Z, family = poisson(), data = dat,
random = ~ Z, ti = time_idx, control = mssm_control(
n_threads = 5L, N_part = 500L, what = "log_density"))
ll_func_anti <- mssm(
fixed = y ~ X1 + X2 + Z, family = poisson(), data = dat,
random = ~ Z, ti = time_idx, control = mssm_control(
n_threads = 5L, N_part = 500L, what = "log_density",
use_antithetic = TRUE))
no_anti <- replicate(
100, {
ti <- system.time(x <- logLik(ll_func_no_anti$pf_filter(
cfix = cfix, disp = numeric(), F. = F., Q = Q, seed = NULL)))
list(ti = ti, x = x)
}, simplify = FALSE)
w_anti <- replicate(
100, {
ti <- system.time(x <- logLik(ll_func_anti$pf_filter(
cfix = cfix, disp = numeric(), F. = F., Q = Q, seed = NULL)))
list(ti = ti, x = x)
}, simplify = FALSE)
list(no_anti = no_anti, w_anti = w_anti)
})The mean estimate of the log-likelihood and standard error of the estimate is shown below with and without antithetic variables.
sapply(compare_anti, function(x){
x <- sapply(x, "[[", "x")
c(mean = mean(x), se = sd(x) / sqrt(length(x)))
})## no_anti w_anti
## mean -5864.42610 -5864.3495
## se 0.05163 0.0298Using antithetic variables is slower. Below we show summary statistics for the elapsed time without using antithetic variables and with antithetic variables.
sapply(compare_anti, function(x){
x <- sapply(x, "[[", "ti")
z <- x[c("elapsed"), ]
c(mean = mean(z), quantile(z, c(.5, .25, .75, 0, 1)))
})## no_anti w_anti
## mean 0.4878 0.5402
## 50% 0.4810 0.5340
## 25% 0.4695 0.5207
## 75% 0.4993 0.5553
## 0% 0.4400 0.4910
## 100% 0.5740 0.6560We will need to estimate the parameters for real applications. We could do this e.g., with a Monte Carlo expectation-maximization algorithm or by using a Monte Carlo approximation of the gradient. Currently, the latter is only available and the user will have to write a custom function to perform the estimation. I will provide an example below. The sgd function is not a part of the package. Instead the package provides a way to approximate the gradient and allows the user to perform subsequent maximization (e.g., with constraints or penalties). The definition of the sgd is given at the end of this file as it is somewhat long. We start by using a Laplace approximation to get the starting values.
# setup mssmFunc object to use
ll_func <- mssm(
fixed = y ~ X1 + X2 + Z, family = poisson(), data = dat,
random = ~ Z, ti = time_idx, control = mssm_control(
n_threads = 5L, N_part = 200L, what = "gradient", use_antithetic = TRUE))
# use Laplace approximation to get starting values
system.time(
sta <- ll_func$Laplace(
F. = diag(.5, 2), Q = diag(1, 2), cfix = coef(glm_fit), disp = numeric()))## Mode approxmation failed at least once
## user system elapsed
## 31.220 0.636 7.832# the function returns an object with the estimated parameters and
# approximation log-likelihood
sta##
## Call: mssm(fixed = y ~ X1 + X2 + Z, family = poisson(), data = dat,
## random = ~Z, ti = time_idx, control = mssm_control(n_threads = 5L,
## N_part = 200L, what = "gradient", use_antithetic = TRUE))
##
## Family is 'poisson' with link 'log'.
## Parameters are estimated with a Laplace approximation.
## State vector is assumed to be X_t ~ N(F * X_(t-1), Q).
##
## F estimate is
## (Intercept) Z
## (Intercept) 0.49174 -0.00466
## Z -0.00831 0.79513
##
## Q's standard deviations estimates are
## (Intercept) Z
## 0.547 0.703
##
## Q's correlation matrix estimates is (lower triangle is shown)
## (Intercept)
## Z 0.325
##
## Fixed coefficients estimates are
## (Intercept) X1 X2 Z
## -0.910 0.213 0.523 -0.892
##
## Log-likelihood approximation is -5863
## Number of parameters 11
## Number of observations 6242## (Intercept) Z
## (Intercept) 0.2996 0.1251
## Z 0.1251 0.4940# use stochastic gradient descent with averaging
set.seed(25164416)
system.time(
res <- sgd(
ll_func, F. = sta$F., Q = sta$Q, cfix = sta$cfix,
lrs = .001 * (1:50)^(-1/2), n_it = 50L, avg_start = 30L))## user system elapsed
## 227.520 1.236 53.674# use Adam algorithm instead
set.seed(25164416)
system.time(
resa <- adam(
ll_func, F. = sta$F., Q = sta$Q, cfix = sta$cfix,
lr = .01, n_it = 50L))## user system elapsed
## 227.604 1.283 53.607Plots of the approximate log-likelihoods at each iteration is shown below along with the final estimates.
## [1] -5862.05 -5861.92 -5861.79 -5861.78 -5861.54 -5861.59

## (Intercept) Z
## (Intercept) 0.4957314 -0.001611
## Z -0.0007354 0.799463## (Intercept) Z
## (Intercept) 0.3031 0.1243
## Z 0.1243 0.4970## [1] -0.9740 0.2137 0.5240 -0.8984# compare with output from Adam algorithm
print(tail(resa$logLik), digits = 6) # final log-likelihood approximations## [1] -5862.07 -5861.94 -5861.81 -5861.79 -5861.56 -5861.65

## (Intercept) Z
## (Intercept) 0.4931484 -0.002659
## Z 0.0001808 0.800192## (Intercept) Z
## (Intercept) 0.3069 0.1300
## Z 0.1300 0.4987## [1] -0.9840 0.2136 0.5245 -0.9396We may want to use more particles towards the end when we estimate the parameters. To do, we use the approximation described in the next section at the final estimates that we arrived at before.
ll_func <- mssm(
fixed = y ~ X1 + X2 + Z, family = poisson(), data = dat,
random = ~ Z, ti = time_idx, control = mssm_control(
n_threads = 5L, N_part = 10000L, what = "gradient",
which_ll_cp = "KD", aprx_eps = .01, use_antithetic = TRUE))
set.seed(25164416)
system.time(
res_final <- adam(
ll_func, F. = resa$F., Q = resa$Q, cfix = resa$cfix,
lr = .001, n_it = 25L))## user system elapsed
## 2962.58 24.67 674.59
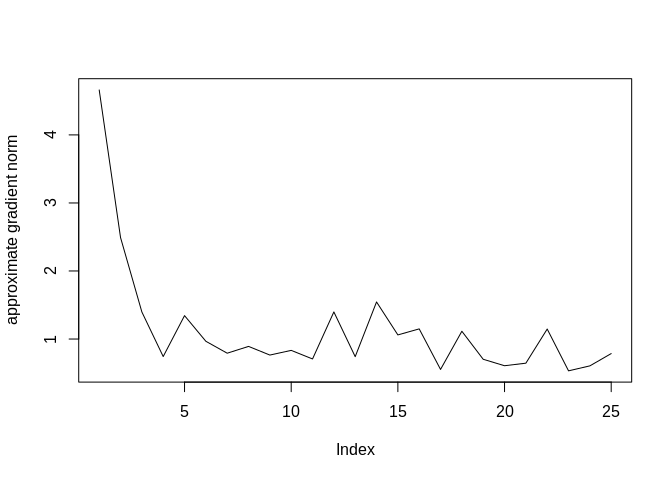
## (Intercept) Z
## (Intercept) 0.502139 -0.002061
## Z 0.007066 0.799001## (Intercept) Z
## (Intercept) 0.3032 0.1228
## Z 0.1228 0.4969## [1] -0.9784 0.2136 0.5245 -0.9187One drawback with the particle filter we use is that it has computational complexity where is the number of particles. We can see this by changing the number of particles.
local({
# assign function that returns a function that uses a given number of
# particles
func <- function(N){
ll_func <- mssm(
fixed = y ~ X1 + X2 + Z, family = poisson(), data = dat,
random = ~ Z, ti = time_idx, control = mssm_control(
n_threads = 5L, N_part = N, what = "log_density",
use_antithetic = TRUE))
function()
ll_func$pf_filter(
cfix = coef(glm_fit), disp = numeric(), F. = diag(1e-8, 2),
Q = diag(1e-4^2, 2))
}
f_100 <- func( 100L)
f_200 <- func( 200L)
f_400 <- func( 400L)
f_800 <- func( 800L)
f_1600 <- func(1600L)
# benchmark. Should ĩncrease at ~ N^2 rate
microbenchmark::microbenchmark(
`100` = f_100(), `200` = f_200(), `400` = f_400(), `800` = f_800(),
`1600` = f_1600(), times = 3L)
})## Unit: milliseconds
## expr min lq mean median uq max neval
## 100 68.76 69.48 69.86 70.2 70.42 70.63 3
## 200 147.95 153.14 159.71 158.3 165.59 172.86 3
## 400 367.42 370.75 372.86 374.1 375.58 377.09 3
## 800 973.96 974.70 996.01 975.4 1007.03 1038.61 3
## 1600 3268.12 3290.25 3304.28 3312.4 3322.36 3332.33 3A solution is to use the dual k-d tree method I cover later. The computational complexity is for this method which is somewhat indicated by the run times shown below.
local({
# assign function that returns a function that uses a given number of
# particles
func <- function(N){
ll_func <- mssm(
fixed = y ~ X1 + X2 + Z, family = poisson(), data = dat,
random = ~ Z, ti = time_idx, control = mssm_control(
n_threads = 5L, N_part = N, what = "log_density",
which_ll_cp = "KD", KD_N_max = 6L, aprx_eps = 1e-2,
use_antithetic = TRUE))
function()
ll_func$pf_filter(
cfix = coef(glm_fit), disp = numeric(), F. = diag(1e-8, 2),
Q = diag(1e-4^2, 2))
}
f_100 <- func( 100L)
f_200 <- func( 200L)
f_400 <- func( 400L)
f_800 <- func( 800L)
f_1600 <- func( 1600L)
f_12800 <- func(12800L) # <-- much larger
# benchmark. Should increase at ~ N log N rate
microbenchmark::microbenchmark(
`100` = f_100(), `200` = f_200(), `400` = f_400(), `800` = f_800(),
`1600` = f_1600(), `12800` = f_12800(), times = 3L)
})## Unit: milliseconds
## expr min lq mean median uq max neval
## 100 123.1 124.9 127.2 126.6 129.3 131.9 3
## 200 214.3 215.1 216.4 216.0 217.5 219.0 3
## 400 451.1 452.1 453.1 453.1 454.0 455.0 3
## 800 909.7 917.3 924.3 924.9 931.6 938.2 3
## 1600 1663.5 1693.8 1708.2 1724.1 1730.6 1737.1 3
## 12800 9243.3 9261.2 9272.7 9279.1 9287.5 9295.8 3The aprx_eps controls the size of the error. To be precise about what this value does then we need to some notation for the complete likelihood (the likelihood where we observe s). This is
where is conditional distribution given , is the conditional distribution of given , and is the time-invariant distribution of . Let be the weight of particle at time and be the th particle at time . Then we ensure the error in our evaluation of terms never exceeds
where and are respectively an upper and lower bound of . The question is how big the error is. Thus, we consider the error in the log-likelihood approximation at the true parameters.
ll_compare <- local({
N_use <- 500L
# we alter the seed in each run. First, the exact method
ll_no_approx <- sapply(1:200, function(seed){
ll_func <- mssm(
fixed = y ~ X1 + X2 + Z, family = poisson(), data = dat,
random = ~ Z, ti = time_idx, control = mssm_control(
n_threads = 5L, N_part = N_use, what = "log_density",
seed = seed, use_antithetic = TRUE))
logLik(ll_func$pf_filter(
cfix = cfix, disp = numeric(), F. = F., Q = Q))
})
# then the approximation
ll_approx <- sapply(1:200, function(seed){
ll_func <- mssm(
fixed = y ~ X1 + X2 + Z, family = poisson(), data = dat,
random = ~ Z, ti = time_idx, control = mssm_control(
n_threads = 5L, N_part = N_use, what = "log_density",
KD_N_max = 6L, aprx_eps = 1e-2, seed = seed,
which_ll_cp = "KD", use_antithetic = TRUE))
logLik(ll_func$pf_filter(
cfix = cfix, disp = numeric(), F. = F., Q = Q))
})
list(ll_no_approx = ll_no_approx, ll_approx = ll_approx)
})par(mar = c(5, 4, 1, 1))
hist(
ll_compare$ll_no_approx, main = "", breaks = 20L,
xlab = "Log-likelihood approximation -- no aprox")
hist(
ll_compare$ll_approx , main = "", breaks = 20L,
xlab = "Log-likelihood approximation -- aprox")
We can make a t-test for whether there is a difference between the two log-likelihood estimates
##
## Welch Two Sample t-test
##
## data: ll_no_approx and ll_approx
## t = -14, df = 398, p-value <2e-16
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -0.5129 -0.3847
## sample estimates:
## mean of x mean of y
## -5864 -5864The fact that there may only be a small difference if any is nice because now we can get a much better approximation (in terms of variance) quickly of e.g., the log-likelihood as shown below.
ll_approx <- sapply(1:10, function(seed){
N_use <- 10000L # many more particles
ll_func <- mssm(
fixed = y ~ X1 + X2 + Z, family = poisson(), data = dat,
random = ~ Z, ti = time_idx, control = mssm_control(
n_threads = 5L, N_part = N_use, what = "log_density",
KD_N_max = 100L, aprx_eps = 1e-2, seed = seed,
which_ll_cp = "KD", use_antithetic = TRUE))
logLik(ll_func$pf_filter(
cfix = cfix, disp = numeric(), F. = F., Q = Q))
})
# approximate log-likelihood
sd(ll_approx)## [1] 0.07152## [1] -5864## [1] 0.3263## [1] -5864.33Next, we look at approximating the observed information matrix with the method suggested by Poyiadjis, Doucet, and Singh (2011).
ll_func <- mssm(
fixed = y ~ X1 + X2 + Z, family = poisson(), data = dat,
random = ~ Z, ti = time_idx, control = mssm_control(
n_threads = 5L, N_part = 10000L, what = "Hessian",
which_ll_cp = "KD", aprx_eps = .01, use_antithetic = TRUE))
set.seed(46658529)
system.time(
mssm_obs_info <- ll_func$pf_filter(
cfix = res_final$cfix, disp = numeric(), F. = res_final$F.,
Q = res_final$Q))## user system elapsed
## 352.638 1.183 77.434We define a function below to get the approximate gradient and approximate observed information matrix from the returned object. Then we compare the output to the GLM we estimated and to the true parameters.
# Function to subtract the approximate gradient elements and approximate
# observed information matrix.
#
# Args:
# object: an object of class mssm.
#
# Returns:
# list with the approximate gradient elements and approximate observed
# information matrix.
get_grad_n_obs_info <- function(object){
stopifnot(inherits(object, "mssm"))
# get dimension of the components
n_rng <- nrow(object$Z)
dim_fix <- nrow(object$X)
dim_rng <- n_rng * n_rng + ((n_rng + 1L) * n_rng) / 2L
has_dispersion <-
any(sapply(c("^Gamma", "^gaussian"), grepl, x = object$family))
# get quantities for each particle
quants <- tail(object$pf_output, 1L)[[1L]]$stats
ws <- exp(tail(object$pf_output, 1L)[[1L]]$ws_normalized)
# get mean estimates
meas <- colSums(t(quants) * drop(ws))
# separate out the different components. Start with the gradient
idx <- dim_fix + dim_rng + has_dispersion
grad <- meas[1:idx]
dim_names <- names(grad)
# then the observed information matrix
I1 <- matrix(
meas[-(1:idx)], dim_fix + dim_rng + has_dispersion,
dimnames = list(dim_names, dim_names))
I2 <- matrix(0., nrow(I1), ncol(I1))
for(i in seq_along(ws))
I2 <- I2 + ws[i] * tcrossprod(quants[1:idx, i])
list(grad = grad, obs_info = tcrossprod(grad) - I1 - I2)
}
# use function
out <- get_grad_n_obs_info(mssm_obs_info)
# approximate gradient
out$grad## (Intercept) X1
## 0.211341 0.283541
## X2 Z
## 0.154870 0.037114
## F:(Intercept).(Intercept) F:Z.(Intercept)
## 0.080264 -0.236594
## F:(Intercept).Z F:Z.Z
## -0.002054 0.410972
## Q:(Intercept).(Intercept) Q:Z.(Intercept)
## -0.361656 0.654905
## Q:Z.Z
## -0.186215## (Intercept) X1
## 0.04401 0.02815
## X2 Z
## 0.02920 0.08919
## F:(Intercept).(Intercept) F:Z.(Intercept)
## 0.06737 0.09086
## F:(Intercept).Z F:Z.Z
## 0.03278 0.04176
## Q:(Intercept).(Intercept) Q:Z.(Intercept)
## 0.03625 0.03951
## Q:Z.Z
## 0.07010# look at output for parameters in the observational equation. First, compare
# with glm's standard errors
sqrt(diag(vcov(glm_fit)))## (Intercept) X1 X2 Z
## 0.01803 0.02654 0.02747 0.02860# and relative to true parameters vs. estimated
rbind(
true = cfix,
glm = coef(glm_fit),
mssm = res_final$cfix,
`standard error` = ses[1:4])## (Intercept) X1 X2 Z
## true -1.00000 0.20000 0.5000 -1.00000
## glm -0.55576 0.20237 0.5160 -0.91216
## mssm -0.97837 0.21359 0.5245 -0.91867
## standard error 0.04401 0.02815 0.0292 0.08919# next look at parameters in state equation. First four are for F.
rbind(
true = c(F.),
mssm = c(res_final$F.),
`standard error` = ses[5:8])## F:(Intercept).(Intercept) F:Z.(Intercept) F:(Intercept).Z
## true 0.50000 0.100000 0.000000
## mssm 0.50214 0.007066 -0.002061
## standard error 0.06737 0.090857 0.032778
## F:Z.Z
## true 0.80000
## mssm 0.79900
## standard error 0.04176# next three are w.r.t. the lower diagonal part of Q
rbind(
true = Q[lower.tri(Q, diag = TRUE)],
mssm = res_final$Q[lower.tri(Q, diag = TRUE)],
`standard error` = ses[9:11])## Q:(Intercept).(Intercept) Q:Z.(Intercept) Q:Z.Z
## true 0.25000 0.10000 0.4900
## mssm 0.30322 0.12282 0.4969
## standard error 0.03625 0.03951 0.0701The following families are supported:
This package contains a simple implementation of the dual-tree method like the one suggested by Gray and Moore (2003) and shown in Klaas et al. (2006). The problem we want to solve is the sum-kernel problem in Klaas et al. (2006). Particularly, we consider the situation where we have query particles denoted by and source particles denoted by . For each query particle, we want to compute the weights
where each source particle has an associated weight and is a kernel. Computing the above is which is major bottleneck if and is large. However, one can use a k-d tree for the query particles and source particles and exploit that:
Thus, a substantial amount of computation can be skipped or approximated with e.g., the centroid in the source node with only a minor loss of precision. The dual-tree approximation method is and . We start by defining a function to simulate the source and query particles (we will let the two sets be identical for simplicity). Further, we plot one draw of simulated points and illustrate the leafs in the k-d tree.
######
# define function to simulate data
mus <- matrix(c(-1, -1,
1, 1,
-1, 1), 3L, byrow = FALSE)
mus <- mus * .75
Sig <- diag(c(.5^2, .25^2))
get_sims <- function(n_per_grp){
# simulate X
sims <- lapply(1:nrow(mus), function(i){
mu <- mus[i, ]
X <- matrix(rnorm(n_per_grp * 2L), nrow = 2L)
X <- t(crossprod(chol(Sig), X) + mu)
data.frame(X, grp = i)
})
sims <- do.call(rbind, sims)
X <- t(as.matrix(sims[, c("X1", "X2")]))
# simulate weights
ws <- exp(rnorm(ncol(X)))
ws <- ws / sum(ws)
list(sims = sims, X = X, ws = ws)
}
#####
# show example
set.seed(42452654)
invisible(list2env(get_sims(5000L), environment()))
# plot points
par(mar = c(5, 4, 1, 1))
plot(as.matrix(sims[, c("X1", "X2")]), col = sims$grp + 1L)
# find k-d tree and add borders
out <- mssm:::test_KD_note(X, 50L)
out$indices <- out$indices + 1L
n_ele <- drop(out$n_elems)
idx <- mapply(`:`, cumsum(c(1L, head(n_ele, -1))), cumsum(n_ele))
stopifnot(all(sapply(idx, length) == n_ele))
idx <- lapply(idx, function(i) out$indices[i])
stopifnot(!anyDuplicated(unlist(idx)), length(unlist(idx)) == ncol(X))
grps <- lapply(idx, function(i) X[, i])
borders <- lapply(grps, function(x) apply(x, 1, range))
invisible(lapply(borders, function(b)
rect(b[1, "X1"], b[1, "X2"], b[2, "X1"], b[2, "X2"])))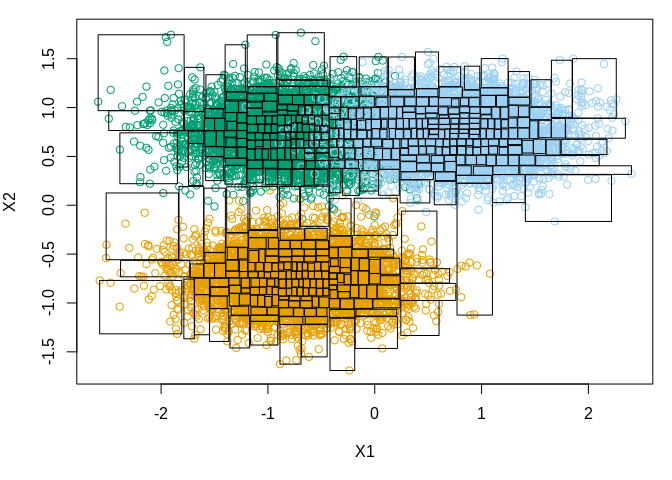
Next, we compute the run-times for the previous examples and compare the approximations of the un-normalized log weights, , and normalized weights, . The n_threads sets the number of threads to use in the methods.
# run-times
microbenchmark::microbenchmark(
`dual tree 1` = mssm:::FSKA (X = X, ws = ws, Y = X, N_min = 10L,
eps = 5e-3, n_threads = 1L),
`dual tree 4` = mssm:::FSKA (X = X, ws = ws, Y = X, N_min = 10L,
eps = 5e-3, n_threads = 4L),
`naive 1` = mssm:::naive(X = X, ws = ws, Y = X, n_threads = 1L),
`naive 4` = mssm:::naive(X = X, ws = ws, Y = X, n_threads = 4L),
times = 10L)## Unit: milliseconds
## expr min lq mean median uq max neval
## dual tree 1 109.58 114.52 126.6 115.53 118.07 232.78 10
## dual tree 4 40.79 41.55 47.2 43.36 48.48 66.86 10
## naive 1 3263.74 3523.12 3556.4 3556.02 3647.89 3743.59 10
## naive 4 898.78 976.93 1335.7 1138.00 1286.56 3342.69 10# The functions return the un-normalized log weights. We first compare
# the result on this scale
o1 <- mssm:::FSKA (X = X, ws = ws, Y = X, N_min = 10L, eps = 5e-3,
n_threads = 1L)
o2 <- mssm:::naive(X = X, ws = ws, Y = X, n_threads = 4L)
all.equal(o1, o2)## [1] "Mean relative difference: 0.0015"par(mar = c(5, 4, 1, 1))
hist((o1 - o2)/ abs((o1 + o2) / 2), breaks = 50, main = "",
xlab = "Delta un-normalized log weights")
# then we compare the normalized weights
func <- function(x){
x_max <- max(x)
x <- exp(x - x_max)
x / sum(x)
}
o1 <- func(o1)
o2 <- func(o2)
all.equal(o1, o2)## [1] "Mean relative difference: 0.0008531"
Finally, we compare the run-times as function of . The dashed line is “naive” method, the continuous line is the dual-tree method, and the dotted line is dual-tree method using 1 thread.
Ns <- 2^(7:14)
run_times <- lapply(Ns, function(N){
invisible(list2env(get_sims(N), environment()))
microbenchmark::microbenchmark(
`dual-tree` = mssm:::FSKA (X = X, ws = ws, Y = X, N_min = 10L, eps = 5e-3,
n_threads = 4L),
naive = mssm:::naive(X = X, ws = ws, Y = X, n_threads = 4L),
`dual-tree 1` = mssm:::FSKA (X = X, ws = ws, Y = X, N_min = 10L, eps = 5e-3,
n_threads = 1L),
times = 5L)
})
Ns_xtra <- 2^(15:19)
run_times_xtra <- lapply(Ns_xtra, function(N){
invisible(list2env(get_sims(N), environment()))
microbenchmark::microbenchmark(
`dual-tree` = mssm:::FSKA (X = X, ws = ws, Y = X, N_min = 10L, eps = 5e-3,
n_threads = 4L),
times = 5L)
}) library(microbenchmark)
meds <- t(sapply(run_times, function(x) summary(x, unit = "s")[, "median"]))
meds_xtra <-
sapply(run_times_xtra, function(x) summary(x, unit = "s")[, "median"])
meds <- rbind(meds, cbind(meds_xtra, NA_real_, NA_real_))
dimnames(meds) <- list(
N = c(Ns, Ns_xtra) * 3L, method = c("Dual-tree", "Naive", "Dual-tree 1"))
meds## method
## N Dual-tree Naive Dual-tree 1
## 384 0.001715 0.001659 0.003271
## 768 0.003062 0.002737 0.006856
## 1536 0.005478 0.009643 0.011102
## 3072 0.010753 0.051587 0.026246
## 6144 0.022150 0.166788 0.049191
## 12288 0.035632 0.665132 0.092363
## 24576 0.062067 2.560118 0.173363
## 49152 0.114004 10.363843 0.330979
## 98304 0.220485 NA NA
## 196608 0.481767 NA NA
## 393216 0.921783 NA NA
## 786432 1.824274 NA NA
## 1572864 3.924601 NA NApar(mar = c(5, 4, 1, 1))
matplot(c(Ns, Ns_xtra) * 3L, meds, lty = 1:3, type = "l", log = "xy",
ylab = "seconds", xlab = "N", col = "black")
# Stochastic gradient descent for mssm object. The function assumes that the
# state vector is stationary. The default values are rather arbitrary.
#
# Args:
# object: an object of class mssmFunc.
# n_it: number of iterations.
# lrs: learning rates to use. Must have n_it elements. Like problem specific.
# avg_start: index to start averaging. See Polyak et al. (1992) for arguments
# for averaging.
# cfix: starting values for fixed coefficients.
# F.: starting value for transition matrix in conditional distribution of the
# current state given the previous state.
# Q: starting value for covariance matrix in conditional distribution of the
# current state given the previous.
# verbose: TRUE if output should be printed during estmation.
# disp: starting value for dispersion parameter.
#
# Returns:
# List with estimates and the log-likelihood approximation at each iteration.
sgd <- function(
object, n_it = 150L,
lrs = 1e-2 * (1:n_it)^(-1/2), avg_start = max(1L, as.integer(n_it * 4L / 5L)),
cfix, F., Q, verbose = FALSE, disp = numeric())
{
# make checks
stopifnot(
inherits(object, "mssmFunc"), object$control$what == "gradient", n_it > 0L,
all(lrs > 0.), avg_start > 1L, length(lrs) == n_it)
n_fix <- nrow(object$X)
n_rng <- nrow(object$Z)
# objects for estimates at each iteration, gradient norms, and
# log-likelihood approximations
has_dispersion <-
any(sapply(c("^Gamma", "^gaussian"), grepl, x = object$family))
n_params <-
has_dispersion + n_fix + n_rng * n_rng + n_rng * (n_rng + 1L) / 2L
ests <- matrix(NA_real_, n_it + 1L, n_params)
ests[1L, ] <- c(
cfix, if(has_dispersion) disp else NULL, F.,
Q[lower.tri(Q, diag = TRUE)])
grad_norm <- lls <- rep(NA_real_, n_it)
# indices of the different components
idx_fix <- 1:n_fix
if(has_dispersion)
idx_dip <- n_fix + 1L
idx_F <- 1:(n_rng * n_rng) + n_fix + has_dispersion
idx_Q <- 1:(n_rng * (n_rng + 1L) / 2L) + n_fix + n_rng * n_rng +
has_dispersion
# function to set the parameters
library(matrixcalc) # TODO: get rid of this
dup_mat <- duplication.matrix(ncol(Q))
set_parems <- function(i){
# select whether or not to average
idx <- if(i > avg_start) avg_start:i else i
# set new parameters
cfix <<- colMeans(ests[idx, idx_fix, drop = FALSE])
if(has_dispersion)
disp <<- colMeans(ests[idx, idx_dip, drop = FALSE])
F.[] <<- colMeans(ests[idx, idx_F , drop = FALSE])
Q[] <<- dup_mat %*% colMeans(ests[idx, idx_Q , drop = FALSE])
}
# run algorithm
max_half <- 25L
for(i in 1:n_it + 1L){
# get gradient. First, run the particle filter
filter_out <- object$pf_filter(
cfix = cfix, disp = disp, F. = F., Q = Q, seed = NULL)
lls[i - 1L] <- c(logLik(filter_out))
# then get the gradient associated with each particle and the log
# normalized weight of the particles
grads <- tail(filter_out$pf_output, 1L)[[1L]]$stats
ws <- tail(filter_out$pf_output, 1L)[[1L]]$ws_normalized
# compute the gradient and take a small step
grad <- colSums(t(grads) * drop(exp(ws)))
grad_norm[i - 1L] <- norm(t(grad))
lr_i <- lrs[i - 1L]
k <- 0L
while(k < max_half){
ests[i, ] <- ests[i - 1L, ] + lr_i * grad
set_parems(i)
# check that Q is positive definite and the system is stationary
c1 <- all(abs(eigen(F.)$values) < 1)
c2 <- all(eigen(Q)$values > 0)
c3 <- !has_dispersion || disp > 0.
if(c1 && c2 && c3)
break
# decrease learning rate
lr_i <- lr_i * .5
k <- k + 1L
}
# check if we failed to find a value within our constraints
if(k == max_half)
stop("failed to find solution within constraints")
# print information if requested
if(verbose){
cat(sprintf(
"\nIt %5d: log-likelihood (current, max) %12.2f, %12.2f\n",
i - 1L, logLik(filter_out), max(lls, na.rm = TRUE)),
rep("-", 66), "\n", sep = "")
cat("cfix\n")
print(cfix)
if(has_dispersion)
cat(sprintf("Dispersion: %20.8f\n", disp))
cat("F\n")
print(F.)
cat("Q\n")
print(Q)
cat(sprintf("Gradient norm: %10.4f\n", grad_norm[i - 1L]))
print(get_ess(filter_out))
}
}
list(estimates = ests, logLik = lls, F. = F., Q = Q, cfix = cfix,
disp = disp, grad_norm = grad_norm)
}
# Stochastic gradient descent for mssm object using the Adam algorithm. The
# function assumes that the state vector is stationary.
#
# Args:
# object: an object of class mssmFunc.
# n_it: number of iterations.
# mp: decay rate for first moment.
# vp: decay rate for secod moment.
# lr: learning rate.
# cfix: starting values for fixed coefficients.
# F.: starting value for transition matrix in conditional distribution of the
# current state given the previous state.
# Q: starting value for covariance matrix in conditional distribution of the
# current state given the previous.
# verbose: TRUE if output should be printed during estmation.
# disp: starting value for dispersion parameter.
#
# Returns:
# List with estimates and the log-likelihood approximation at each iteration.
adam <- function(
object, n_it = 150L, mp = .9, vp = .999, lr = .01, cfix, F., Q,
verbose = FALSE, disp = numeric())
{
# make checks
stopifnot(
inherits(object, "mssmFunc"), object$control$what == "gradient", n_it > 0L,
lr > 0., mp > 0, mp < 1, vp > 0, vp < 1)
n_fix <- nrow(object$X)
n_rng <- nrow(object$Z)
# objects for estimates at each iteration, gradient norms, and
# log-likelihood approximations
has_dispersion <-
any(sapply(c("^Gamma", "^gaussian"), grepl, x = object$family))
n_params <-
has_dispersion + n_fix + n_rng * n_rng + n_rng * (n_rng + 1L) / 2L
ests <- matrix(NA_real_, n_it + 1L, n_params)
ests[1L, ] <- c(
cfix, if(has_dispersion) disp else NULL, F.,
Q[lower.tri(Q, diag = TRUE)])
grad_norm <- lls <- rep(NA_real_, n_it)
# indices of the different components
idx_fix <- 1:n_fix
if(has_dispersion)
idx_dip <- n_fix + 1L
idx_F <- 1:(n_rng * n_rng) + n_fix + has_dispersion
idx_Q <- 1:(n_rng * (n_rng + 1L) / 2L) + n_fix + n_rng * n_rng +
has_dispersion
# function to set the parameters
library(matrixcalc) # TODO: get rid of this
dup_mat <- duplication.matrix(ncol(Q))
set_parems <- function(i){
cfix <<- ests[i, idx_fix]
if(has_dispersion)
disp <<- ests[i, idx_dip]
F.[] <<- ests[i, idx_F ]
Q[] <<- dup_mat %*% ests[i, idx_Q ]
}
# run algorithm
max_half <- 25L
m <- NULL
v <- NULL
failed <- FALSE
for(i in 1:n_it + 1L){
# get gradient. First, run the particle filter
filter_out <- object$pf_filter(
cfix = cfix, disp = disp, F. = F., Q = Q, seed = NULL)
lls[i - 1L] <- c(logLik(filter_out))
# then get the gradient associated with each particle and the log
# normalized weight of the particles
grads <- tail(filter_out$pf_output, 1L)[[1L]]$stats
ws <- tail(filter_out$pf_output, 1L)[[1L]]$ws_normalized
# compute the gradient and take a small step
grad <- colSums(t(grads) * drop(exp(ws)))
grad_norm[i - 1L] <- norm(t(grad))
m <- if(is.null(m)) (1 - mp) * grad else mp * m + (1 - mp) * grad
v <- if(is.null(v)) (1 - vp) * grad^2 else vp * v + (1 - vp) * grad^2
mh <- m / (1 - mp^(i - 1))
vh <- v / (1 - vp^(i - 1))
de <- mh / sqrt(vh + 1e-8)
lr_i <- lr
k <- 0L
while(k < max_half){
ests[i, ] <- ests[i - 1L, ] + lr_i * de
set_parems(i)
# check that Q is positive definite, the dispersion parameter is
# positive, and the system is stationary
c1 <- all(abs(eigen(F.)$values) < 1)
c2 <- all(eigen(Q)$values > 0)
c3 <- !has_dispersion || disp > 0.
if(c1 && c2 && c3)
break
# decrease learning rate
lr_i <- lr_i * .5
k <- k + 1L
}
# check if we failed to find a value within our constraints
if(k == max_half){
warning("failed to find solution within constraints")
failed <- TRUE
break
}
# print information if requested
if(verbose){
cat(sprintf(
"\nIt %5d: log-likelihood (current, max) %12.2f, %12.2f\n",
i - 1L, logLik(filter_out), max(lls, na.rm = TRUE)),
rep("-", 66), "\n", sep = "")
cat("cfix\n")
print(cfix)
if(has_dispersion)
cat(sprintf("Dispersion: %20.8f\n", disp))
cat("F\n")
print(F.)
cat("Q\n")
print(Q)
cat(sprintf("Gradient norm: %10.4f\n", grad_norm[i - 1L]))
print(get_ess(filter_out))
}
}
list(estimates = ests, logLik = lls, F. = F., Q = Q, cfix = cfix,
disp = disp, failed = failed, grad_norm = grad_norm)
}Durbin, J., and S. J. Koopman. 1997. “Monte Carlo Maximum Likelihood Estimation for Non-Gaussian State Space Models.” Biometrika 84 (3). [Oxford University Press, Biometrika Trust]: 669–84. http://www.jstor.org/stable/2337587.
Gray, Alexander G., and Andrew W. Moore. 2003. “Rapid Evaluation of Multiple Density Models.” In AISTATS.
Klaas, Mike, Mark Briers, Nando de Freitas, Arnaud Doucet, Simon Maskell, and Dustin Lang. 2006. “Fast Particle Smoothing: If I Had a Million Particles.” In Proceedings of the 23rd International Conference on Machine Learning, 481–88. ICML ’06. New York, NY, USA: ACM. https://doi.acm.org/10.1145/1143844.1143905.
Lin, Ming T, Junni L Zhang, Qiansheng Cheng, and Rong Chen. 2005. “Independent Particle Filters.” Journal of the American Statistical Association 100 (472). Taylor & Francis: 1412–21. https://doi.org/10.1198/016214505000000349.
Polyak, B., and A. Juditsky. 1992. “Acceleration of Stochastic Approximation by Averaging.” SIAM Journal on Control and Optimization 30 (4): 838–55. https://doi.org/10.1137/0330046.
Poyiadjis, George, Arnaud Doucet, and Sumeetpal S. Singh. 2011. “Particle Approximations of the Score and Observed Information Matrix in State Space Models with Application to Parameter Estimation.” Biometrika 98 (1). Biometrika Trust: 65–80. https://www.jstor.org/stable/29777165.