R package pomdp: Partially Observable Markov Decision Processes

Provides the infrastructure to define and analyze the solutions of Partially Observable Markov Decision Processes (POMDP) models. The package uses the solvers from pomdp-solve (Cassandra, 2015) available in the R package pomdpSolve to solve POMDPs using a variety of algorithms.

The package provides the following algorithms:

• Exact value iteration
  • Enumeration algorithm (Sondik 1971, Mohan 1982).
  • Two pass algorithm (Sondik 1971).
  • Witness algorithm (Littman, Cassandra, Kaelbling 1996).
  • Incremental pruning algorithm (Zhang and Liu 1996, Cassandra et al 1997).
• Approximate value iteration
  • Finite grid algorithm (Cassandra 2015), a variation of point-based value iteration to solve larger POMDPs (PBVI; see Pineau 2003) without dynamic belief set expansion.
  • SARSOP (Kurniawati, Hsu and Lee 2008), point-based algorithm that approximates optimally reachable belief spaces for infinite-horizon problems (via package sarsop).

Installation

Stable CRAN version: install from within R with

install.packages("pomdp")

Current development version: install from GitHub (needs devtools).

devtools::install_github("mhahsler/pomdp")

Usage

Solving the simple infinite-horizon Tiger problem.

library("pomdp")
data("Tiger")
Tiger

## POMDP, list - Tiger Problem
##   Discount factor: 0.75
##   Horizon: Inf epochs
##   List components: 'name', 'discount', 'horizon', 'states', 'actions',
##     'observations', 'transition_prob', 'observation_prob', 'reward',
##     'start', 'terminal_values'

sol <- solve_POMDP(model = Tiger)
sol

## POMDP, list - Tiger Problem
##   Discount factor: 0.75
##   Horizon: Inf epochs
##   Solved:
##     Solution converged: TRUE
##     Total expected reward: 1.933439
##   List components: 'name', 'discount', 'horizon', 'states', 'actions',
##     'observations', 'transition_prob', 'observation_prob', 'reward',
##     'start', 'solution', 'solver_output'

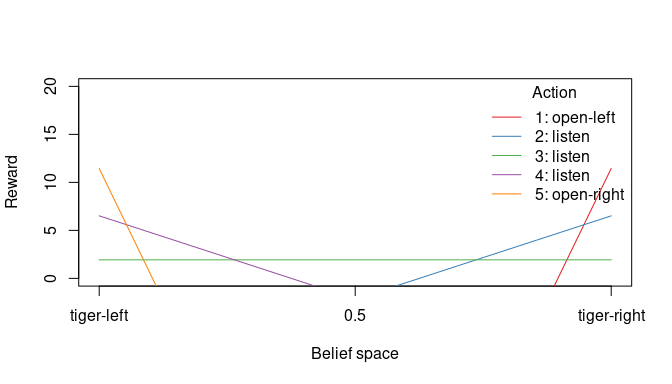
plot_value_function(sol, ylim = c(0, 20))

plot_policy_graph(sol)

References

• Cassandra, A. (2015). pomdp-solve: POMDP Solver Software, http://www.pomdp.org.
• Sondik, E. (1971). The Optimal Control of Partially Observable Markov Processes. Ph.D. Dissertation, Stanford University.
• Cassandra, A., Littman M.L., Zhang L. (1997). Incremental Pruning: A Simple, Fast, Exact Algorithm for Partially Observable Markov Decision Processes. UAI’97: Proceedings of the Thirteenth conference on Uncertainty in artificial intelligence, August 1997, pp. 54-61.
• Monahan, G. E. (1982). A survey of partially observable Markov decision processes: Theory, models, and algorithms. Management Science 28(1):1-16.
• Littman, M. L.; Cassandra, A. R.; and Kaelbling, L. P. (1996). Efficient dynamic-programming updates in partially observable Markov decision processes. Technical Report CS-95-19, Brown University, Providence, RI.
• Zhang, N. L., and Liu, W. (1996). Planning in stochastic domains: Problem characteristics and approximation. Technical Report HKUST-CS96-31, Department of Computer Science, Hong Kong University of Science and Technology.
• Pineau, J., Gordon, G.J., Thrun, S.B. (2003). Point-based value iteration: an anytime algorithm for POMDPs. IJCAI’03: Proceedings of the 18th international joint conference on Artificial Intelligence. Pages 1025-1030.
• Kurniawati, H., Hsu, D., and Lee, W.S. (2008). SARSOP: Efficient point-based POMDP planning by approximating optimally reachable belief spaces. In Proc. Robotics: Science and Systems.

Acknowledgments

Development of this package was supported in part by National Institute of Standards and Technology (NIST) under grant number 60NANB17D180.