pre: an R package for deriving prediction rule ensembles

Contents

• Introduction
• Example: A rule ensemble for predicting ozone levels
• Tools for interpretation
  • Importance measures
  • Explaining individual predictions
  • Partial dependence plots
  • Assessing presence of interactions
  • Correlations between selected terms
• Tuning parameters of function pre
• Dealing with missing values
• Go sparser with relaxed lasso fits
• Generalized Prediction Ensembles: Combining MARS, rules and linear terms
• Credits
• References

Introduction

pre is an R package for deriving prediction rule ensembles for binary, multinomial, (multivariate) continuous, count and survival responses. Input variables may be numeric, ordinal and categorical. An extensive description of the implementation and functionality is provided in Fokkema (2020). The package largely implements the algorithm for deriving prediction rule ensembles as described in Friedman & Popescu (2008), with several adjustments:

1. The package is completely R based, allowing users better access to the results and more control over the parameters used for generating the prediction rule ensemble.
2. The unbiased tree induction algorithms of Hothorn, Hornik, & Zeileis (2006) is used for deriving prediction rules, by default. Alternatively, the (g)lmtree algorithm of Zeileis, Hothorn, & Hornik (2008) can be employed, or the classification and regression tree (CART) algorithm of Breiman, Friedman, Olshen, & Stone (1984).
3. The package supports a wider range of response variable types.
4. The initial ensemble may be generated as a bagged, boosted and/or random forest ensemble.
5. Hinge functions of predictor variables may be included as baselearners, as in the multivariate adaptive regression splines (MARS) approach of Friedman (1991), using function gpe().
6. Tools for explaining individual predictions are provided.

Note that pre is under development, and much work still needs to be done. Below, an introduction the the package is provided. Fokkema (2020) provides an extensive description of the fitting procedures implemented in function pre() and example analyses with more extensive explanations. An extensive introduction aimed at researchers in social sciences is provided in Fokkema & Strobl (2020).

Example: A rule ensemble for predicting ozone levels

To get a first impression of how function pre() works, we will predict Ozone levels using the airquality dataset. We fit a prediction rule ensemble using function pre():

library("pre")
airq <- airquality[complete.cases(airquality), ]
set.seed(42)
airq.ens <- pre(Ozone ~ ., data = airq)

Note that it is necessary to set the random seed, to allow for later replication of results, because the fitting procedure depends on random sampling of training observations.

We can print the resulting ensemble (alternatively, we could use the print method):

airq.ens
#> 
#> Final ensemble with cv error within 1se of minimum: 
#> 
#>   lambda =  3.543968
#>   number of terms = 12
#>   mean cv error (se) = 352.395 (99.13754)
#> 
#>   cv error type : Mean-Squared Error
#> 
#>          rule   coefficient                          description
#>   (Intercept)   68.48270407                                    1
#>       rule191  -10.97368180              Wind > 5.7 & Temp <= 87
#>       rule173  -10.90385519              Wind > 5.7 & Temp <= 82
#>        rule42   -8.79715538              Wind > 6.3 & Temp <= 84
#>       rule204    7.16114781         Wind <= 10.3 & Solar.R > 148
#>        rule10   -4.68646145              Temp <= 84 & Temp <= 77
#>       rule192   -3.34460038  Wind > 5.7 & Temp <= 87 & Day <= 23
#>        rule51   -2.27864287              Wind > 5.7 & Temp <= 84
#>        rule93    2.18465676              Temp > 77 & Wind <= 8.6
#>        rule74   -1.36479545              Wind > 6.9 & Temp <= 84
#>        rule28   -1.15326093              Temp <= 84 & Wind > 7.4
#>        rule25   -0.70818400              Wind > 6.3 & Temp <= 82
#>       rule166   -0.04751152              Wind > 6.9 & Temp <= 82

The first few lines of the printed results provide the penalty parameter value (λ) employed for selecting the final ensemble. By default, the ‘1-SE’ rule is used for selecting λ; this default can be overridden by employing the penalty.par.val argument of the print method and other functions in the package. Note that the printed cross-validated error is calculated using the same data as was used for generating the rules and likely provides an overly optimistic estimate of future prediction error. To obtain a more realistic prediction error estimate, we will use function cvpre() later on.

Next, the printed results provide the rules and linear terms selected in the final ensemble, with their estimated coefficients. For rules, the description column provides the conditions. For linear terms (which were not selected in the current ensemble), the winsorizing points used to reduce the influence of outliers on the estimated coefficient would be printed in the description column. The coefficient column presents the estimated coefficient. These are regression coefficients, reflecting the expected increase in the response for a unit increase in the predictor, keeping all other predictors constant. For rules, the coefficient thus reflects the difference in the expected value of the response when the conditions of the rule are met, compared to when they are not.

Using the plot method, we can plot the rules in the ensemble as simple decision trees. Here, we will request the nine most important baselearners through specification of the nterms argument. Through the cex argument, we specify the size of the node and path labels:

plot(airq.ens, nterms = 9, cex = .5)

Using the coef method, we can obtain the estimated coefficients for each of the baselearners (we only print the first six terms here for space considerations):

coefs <- coef(airq.ens)
coefs[1:6, ]
#>            rule coefficient                  description
#> 201 (Intercept)   68.482704                            1
#> 167     rule191  -10.973682      Wind > 5.7 & Temp <= 87
#> 150     rule173  -10.903855      Wind > 5.7 & Temp <= 82
#> 39       rule42   -8.797155      Wind > 6.3 & Temp <= 84
#> 179     rule204    7.161148 Wind <= 10.3 & Solar.R > 148
#> 10       rule10   -4.686461      Temp <= 84 & Temp <= 77

We can generate predictions for new observations using the predict method (only the first six predicted values are printed here for space considerations):

predict(airq.ens, newdata = airq[1:6, ])
#>        1        2        3        4        7        8 
#> 32.53896 24.22456 24.22456 24.22456 31.38570 24.22456

Using function cvpre(), we can assess the expected prediction error of the fitted PRE through k-fold cross validation (k = 10, by default, which can be overridden through specification of the k argument):

set.seed(43)
airq.cv <- cvpre(airq.ens)
#> $MSE
#>       MSE        se 
#> 369.92747  88.65343 
#> 
#> $MAE
#>       MAE        se 
#> 13.666860  1.290329

The results provide the mean squared error (MSE) and mean absolute error (MAE) with their respective standard errors. These results are saved for later use in aiq.cv$accuracy. The cross-validated predictions, which can be used to compute alternative estimates of predictive accuracy, are saved in airq.cv$cvpreds. The folds to which observations were assigned are saved in airq.cv$fold_indicators.

For tuning the parameters of function pre() so as to obtain optimal predictive accuracy, users are advised to use R package caret. A tutorial is provided as a vignette, accessible by typing vignette("tuning", package = "pre") in R or by going to https://cran.r-project.org/package=pre/vignettes/missingness.html in a browser and clicking on the corresponding link to the vignette.

Tools for interpretation

Package pre provides several additional tools for interpretation of the final ensemble. These may be especially helpful for complex ensembles containing many rules and linear terms.

Importance measures

We can assess the relative importance of input variables as well as baselearners using the importance() function:

imps <- importance(airq.ens, round = 4)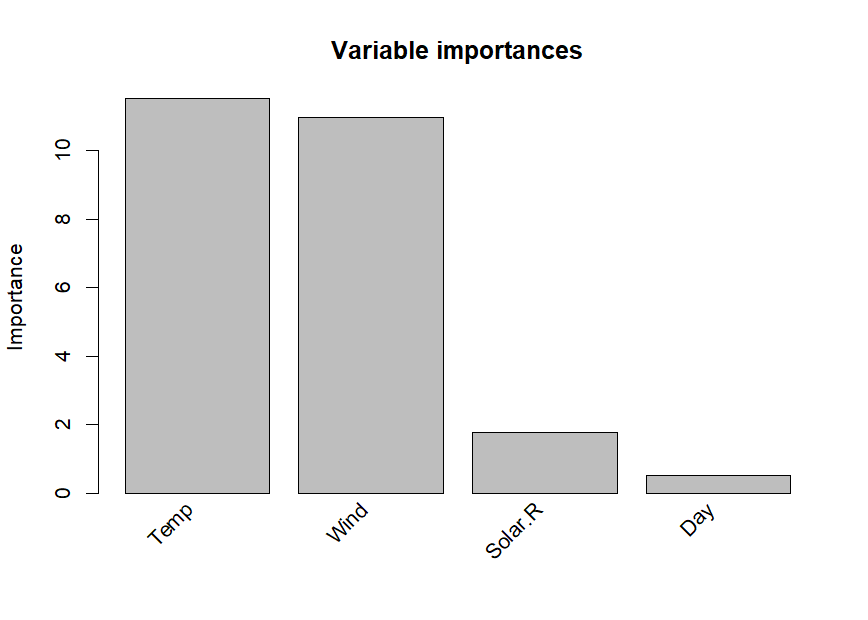

As we already observed in the printed ensemble, the plotted variable importances indicate that Temperature and Wind are most strongly associated with Ozone levels. Solar.R and Day are also associated with Ozone levels, but much less strongly. Variable Month is not plotted, which means it obtained an importance of zero, indicating that it is not associated with Ozone levels. We already observed this in the printed ensemble: Month did not appear in any of the selected terms. The variable and baselearner importances are saved for later use in imps$varimps and imps$baseimps, respectively.

Explaining individual predictions

We can obtain explanations of the predictions for individual observations using function explain():

par(mfrow = c(1, 2))
expl <- explain(airq.ens, newdata = airq[1:2, ], cex = .8)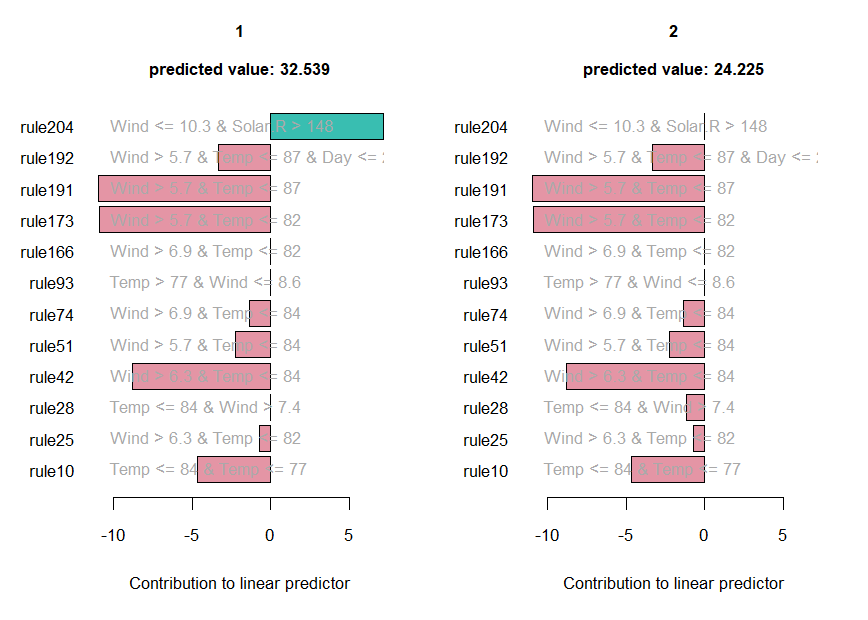

The values of the rules and linear terms for each observation are saved in expl$predictors, their contributions in expl$contribution and the predicted values in expl$predicted.value.

Partial dependence plots

We can obtain partial dependence plots to assess the effect of single predictor variables on the outcome using the singleplot() function:

singleplot(airq.ens, varname = "Temp")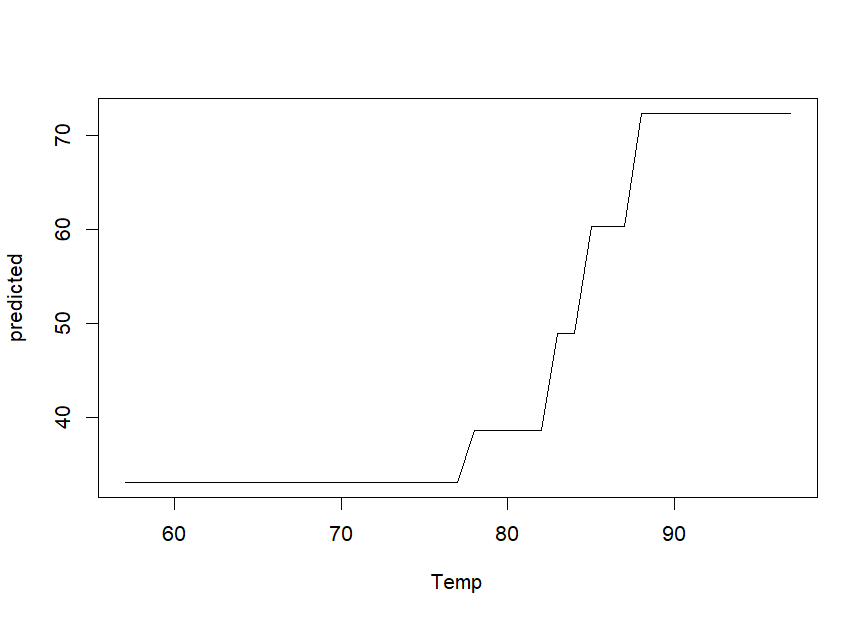

We can obtain partial dependence plots to assess the effects of pairs of predictor variables on the outcome using the pairplot() function:

pairplot(airq.ens, varnames = c("Temp", "Wind"))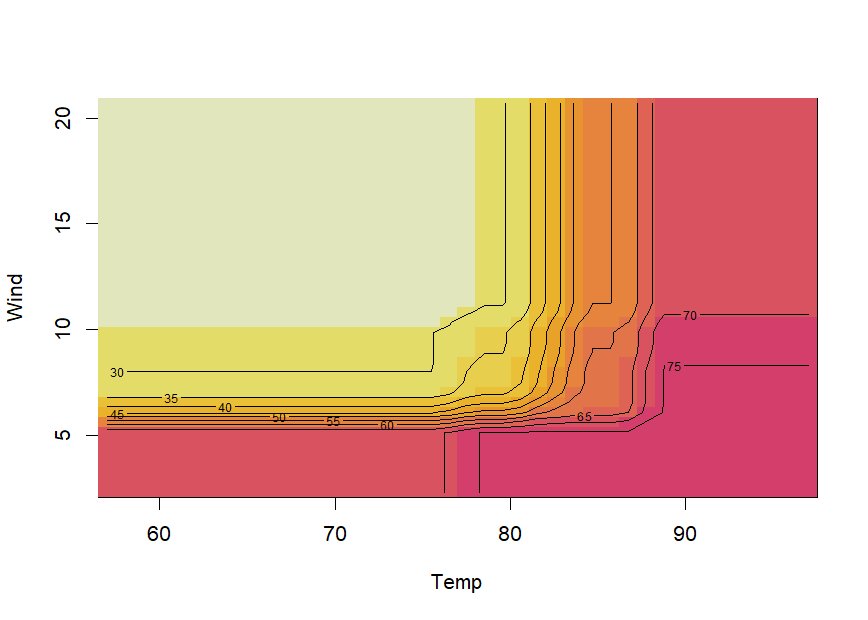

Note that creating partial dependence plots is computationally intensive and computation time will increase fast with increasing numbers of observations and numbers of variables. Milborrow’s (2018) plotmo package provides more efficient functions for plotting partial dependence, which also support pre models.

If the final ensemble does not contain many terms, inspecting individual rules and linear terms through the print method may be more informative than partial dependence plots. One of the main advantages of prediction rule ensembles is their interpretability: the predictive model contains only simple functions of the predictor variables (rules and linear terms), which are easy to grasp. Partial dependence plots are often much more useful for interpretation of complex models, like random forests for example.

Assessing presence of interactions

We can assess the presence of interactions between the input variables using the interact() and bsnullinteract() funtions. Function bsnullinteract() computes null-interaction models (10, by default) based on bootstrap-sampled and permuted datasets. Function interact() computes interaction test statistics for each predictor variables appearing in the specified ensemble. If null-interaction models are provided through the nullmods argument, interaction test statistics will also be computed for the null-interaction model, providing a reference null distribution.

Note that computing null interaction models and interaction test statistics is computationally very intensive, so running the following code will take some time:

set.seed(44)
nullmods <- bsnullinteract(airq.ens)
int <- interact(airq.ens, nullmods = nullmods)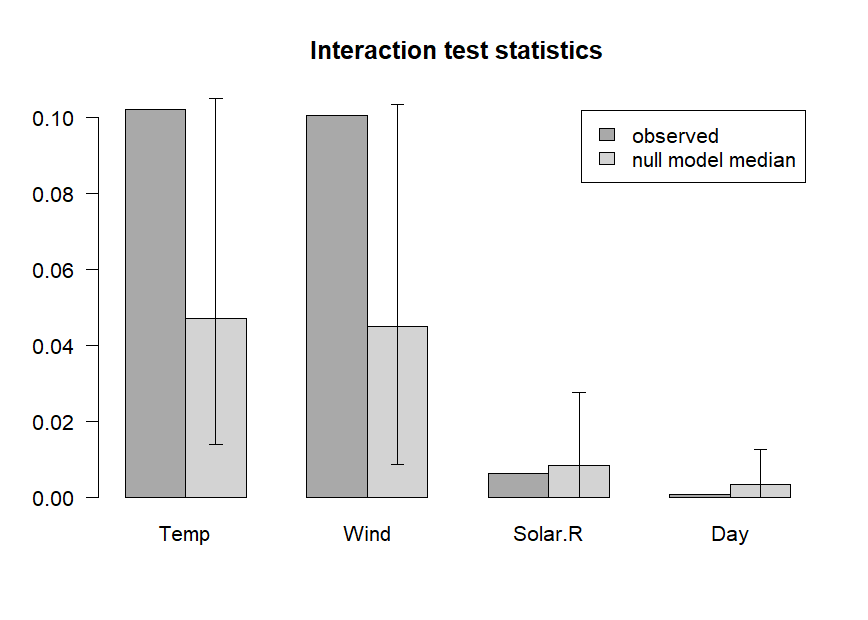

The plotted variable interaction strengths indicate that Temperature and Wind may be involved in interactions, as their observed interaction strengths (darker grey) exceed the upper limit of the 90% confidence interval (CI) of interaction stengths in the null interaction models (lighter grey bar represents the median, error bars represent the 90% CIs). The plot indicates that Solar.R and Day are not involved in any interactions. Note that computation of null interaction models is computationally intensive. A more reliable result can be obtained by computing a larger number of boostrapped null interaction datasets, by setting the nsamp argument of function bsnullinteract() to a larger value (e.g., 100).

Correlations between selected terms

We can assess correlations between the baselearners appearing in the ensemble using the corplot() function:

corplot(airq.ens)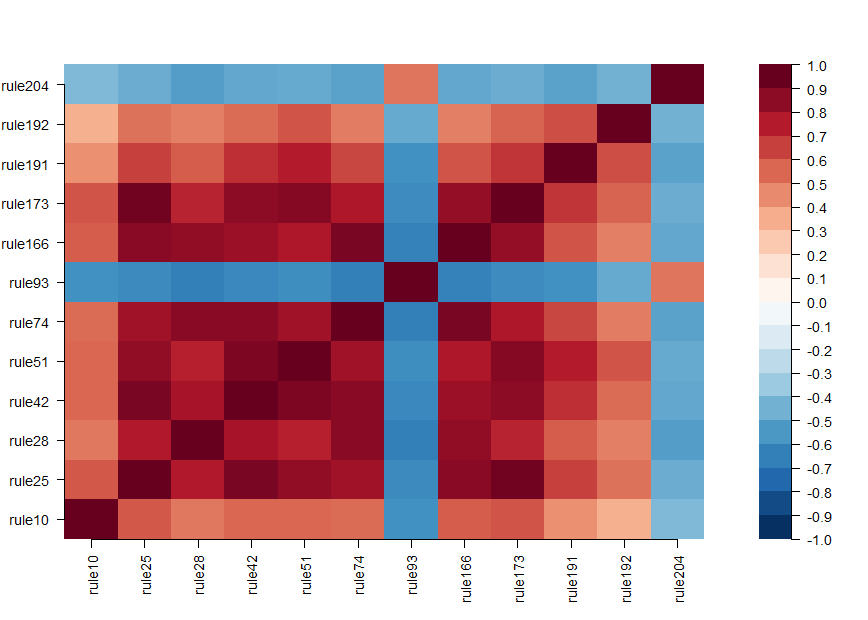

Tuning parameters

To obtain an optimal set of model-fitting parameters, package caret Kuhn (2008) provides a method "pre". For a manual on how to optimize the parameters of function pre using caret’s train function, see the vignette on tuning:

vignette("tuning", package = "pre")

or go to https://cran.r-project.org/package=pre/vignettes/tuning.html in a browser.

Dealing with missing values

Some suggestions on how to deal with missing values are provided in the following vignette:

vignette("missingness", package = "pre")

or go to https://cran.r-project.org/package=pre/vignettes/missingness.html in a browser.

Go sparser with relaxed lasso fits

When sparsity (i.e., a final ensemble comprising only few terms) is of central importance, the so-called relaxed lasso can be employed. It allows for retaining a pre-specified (low) number of terms, with adequate predictive accuracy. An introduction and tutorial is provided in the following vignette:

vignette("relaxed", package = "pre")

Generalized Prediction Ensembles: Combining MARS, rules and linear terms

An even more flexible ensembling approach is implemented in function gpe(), which allows for fitting Generalized Prediction Ensembles: It combines the MARS (multivariate Adaptive Splines) approach of Friedman (1991) with the RuleFit approach of Friedman & Popescu (2008). In other words, gpe() fits an ensemble composed of hinge functions (possibly multivariate), prediction rules and linear functions of the predictor variables. See the following example:

set.seed(42)
airq.gpe <- gpe(Ozone ~ ., data = airquality[complete.cases(airquality),], 
    base_learners = list(gpe_trees(), gpe_linear(), gpe_earth()))
airq.gpe
#> 
#> Final ensemble with cv error within 1se of minimum: 
#> 
#>   lambda =  3.229132
#>   number of terms = 11
#>   mean cv error (se) = 359.2623 (110.8863)
#> 
#>   cv error type : Mean-squared Error
#> 
#>                                   description  coefficient
#>                                   (Intercept)  65.52169488
#>                                    Temp <= 77  -6.20973855
#>                  Wind <= 10.3 & Solar.R > 148   5.46410966
#>                       Wind > 5.7 & Temp <= 82  -8.06127415
#>                       Wind > 5.7 & Temp <= 84  -7.16921733
#>                       Wind > 5.7 & Temp <= 87  -8.04255471
#>           Wind > 5.7 & Temp <= 87 & Day <= 23  -3.40525575
#>                       Wind > 6.3 & Temp <= 82  -2.71925536
#>                       Wind > 6.3 & Temp <= 84  -5.99085126
#>                       Wind > 6.9 & Temp <= 82  -0.04406376
#>                       Wind > 6.9 & Temp <= 84  -0.55827336
#>   eTerm(Solar.R * h(9.7 - Wind), scale = 410)   9.91783320
#> 
#>   'h' in the 'eTerm' indicates the hinge function

The results indicate that several rules, a single hinge (linear spline) function, and no linear terms were selected for the final ensemble. The hinge function and its coefficient indicate that Ozone levels increase with increasing solar radiation and decreasing wind speeds. The prediction rules in the ensemble indicate a similar pattern.

Credits

I am very grateful to package co-author Benjamin Chistoffersen: https://github.com/boennecd, who developed gpe and contributed tremendously by improving functions, code and computational aspects. Furthermore, I am grateful for the many helpful suggestions of Stephen Milborrow, and for the contributions of Karl Holub (https://github.com/holub008) and Advik Shreekumar (https://github.com/adviksh).

References