

fit and compare Species-Area Relationship (SAR) models using multi-model inference
sars provides functionality to fit twenty SAR model using non-linear regression, and to calculate multi-model averaged curves using various information criteria. The software also provides easy to use functionality to plot multi-model SAR curves and to generate confidence intervals using bootstrapping. Additional SAR related functions include fitting the linear version of the power model and comparing parameters with the non-linear version, fitting the general dynamic model of island biogeography, fitting the random placement model to a species abundance-site matrix, and extrapolating fitted SAR models to predict richness on larger islands / sample areas. Version 1.3.0 has added functions for fitting, evaluating and plotting a range of commonly used piecewise SAR models (see Matthews and Rigal (in press) for details on these functions).
As this is version 1.3.5 of the package, it is possible that there are some bugs in places. Please report any issues to us via GitHub.
The package has an associated vignette that provides examples of how to use the package, and an accompanying paper (Matthews et al. 2019).
A website for the package can be found here: https://txm676.github.io/sars/
Version 1.1.1 of the package has been archived on the Zenodo research data repository (DOI: 10.5281/zenodo.2573067).
You can install the released version of sars from CRAN with:
And the development version from GitHub with:
Basic usage of sars will result in using two types of functions:
To fit the power sar model (Arrhenius 1921) to the ‘galapagos’ (Preston 1962) data set:
fit_pow <- sar_power(data = galap)
fit_pow
#>
#> Model:
#> Power
#>
#> Call:
#> S == c * A^z
#>
#> Coefficients:
#> c z
#> 33.1791553 0.2831868Attempting to fit all 20 sar models to the ‘galapagos’ (Preston 1962) data set and get a multi-model SAR:
mm_galap <- sar_average(data = galap)
#>
#> Models to be fitted using a grid start approach:
#>
#> Now attempting to fit the 20 SAR models:
#>
#> -- multi_sars ---------------------------------------------- multi-model SAR --
#> > power : v
#> > powerR : v
#> > epm1 : v
#> > epm2 : v
#> > p1 : v
#> > p2 : v
#> > loga : v
#> > koba : v
#> > monod : v
#> > negexpo : v
#> > chapman : v
#> > weibull3 : v
#> > asymp : v
#> > ratio : v
#> > gompertz : v
#> > weibull4 : v
#> > betap : v
#> > logistic : v
#> > heleg : v
#> > linear : v
#>
#> No model validation checks selected
#>
#> 20 remaining models used to construct the multi SAR:
#> Power, PowerR, Extended Power model 1, Extended Power model 2, Persistence function 1, Persistence function 2, Logarithmic, Kobayashi, Monod, Negative exponential, Chapman Richards, Cumulative Weibull 3 par., Asymptotic regression, Rational function, Gompertz, Cumulative Weibull 4 par., Beta-P cumulative, Logistic(Standard), Heleg(Logistic), Linear model
#> --------------------------------------------------------------------------------Each of the ‘fitted’ objects have corresponding plot methods:
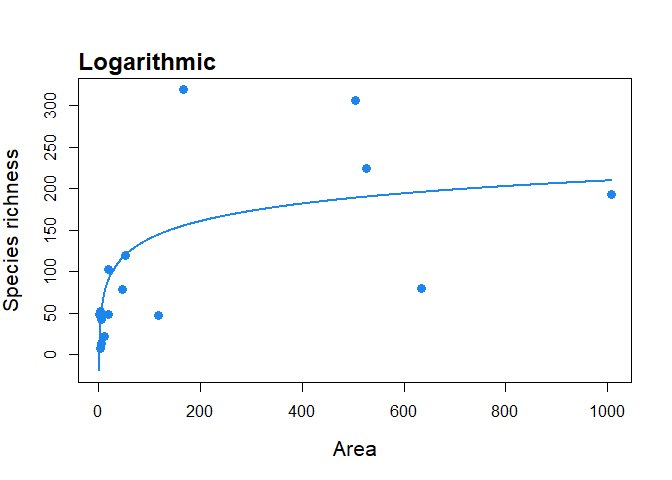
To fit the logarithmic SAR model (Gleason 1922) to the ‘galapagos’ data set and plot it
To fit a multimodel SAR curve to the ‘galapagos’ data set and plot it (alongside the individual model fits)
mm_galap <- suppressMessages(sar_average(data = galap, verb = FALSE))
#>
#> Models to be fitted using a grid start approach:
#>
#> Now attempting to fit the 20 SAR models:
#>
#> -- multi_sars ---------------------------------------------- multi-model SAR --
#> > power : v
#> > powerR : v
#> > epm1 : v
#> > epm2 : v
#> > p1 : v
#> > p2 : v
#> > loga : v
#> > koba : v
#> > monod : v
#> > negexpo : v
#> > chapman : v
#> > weibull3 : v
#> > asymp : v
#> > ratio : v
#> > gompertz : v
#> > weibull4 : v
#> > betap : v
#> > logistic : v
#> > heleg : v
#> > linear : v
#>
#> No model validation checks selected
#>
#> 20 remaining models used to construct the multi SAR:
#> Power, PowerR, Extended Power model 1, Extended Power model 2, Persistence function 1, Persistence function 2, Logarithmic, Kobayashi, Monod, Negative exponential, Chapman Richards, Cumulative Weibull 3 par., Asymptotic regression, Rational function, Gompertz, Cumulative Weibull 4 par., Beta-P cumulative, Logistic(Standard), Heleg(Logistic), Linear model
#> --------------------------------------------------------------------------------
mm_galap
#>
#> This is a sar_average fit object:
#>
#> 20 models successfully fitted
#>
#> AICc used to rank models
plot(mm_galap, pLeg = FALSE, mmSep = TRUE)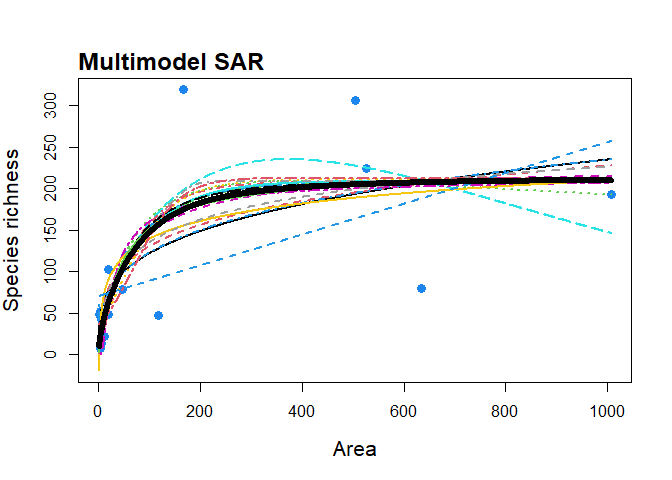
To fit the two-threshold continuous model to the ‘aegean2’ dataset
fit <- sar_threshold(data = aegean2, mod = c("ContTwo"), interval = 0.1,
non_th_models = FALSE, logAxes = "area", con = 1,
logT = log10, nisl = NULL)
plot(fit, cex = 0.8, cex.main = 1.1, cex.lab = 1.1, pcol = "grey") #Figure 1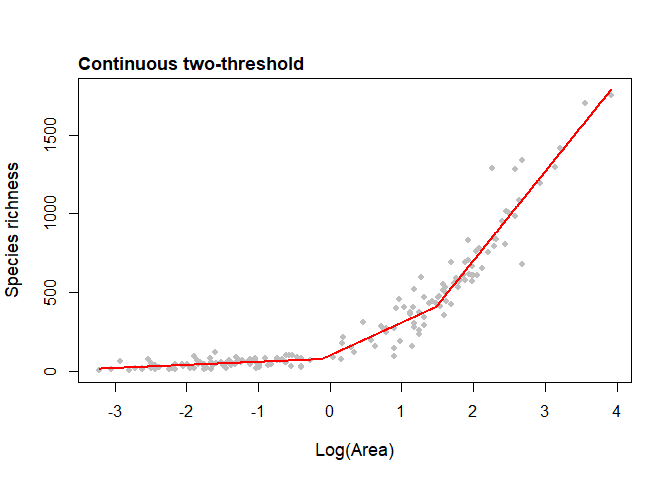
Arrhenius, O. 1921. “Species and Area.” The Journal of Ecology 9 (1): 95. https://doi.org/10.2307/2255763.
Gleason, H. A. 1922. “On the Relation Between Species and Area.” Ecology 3 (2): 158–62. https://doi.org/10.2307/1929150.
Matthews, T. J., and F. Rigal. in press. “Thresholds and the species–area relationship: a set of functions for fitting, evaluating and plotting a range of commonly used piecewise models in R.” Frontiers of Biogeography, in press.
Matthews, T. J., K. A. Triantis, R. J. Whittaker, and F. Guilhaumon. 2019. “sars: an R package for fitting, evaluating and comparing species–area relationship models.” Ecography 42: 1446–55. https://doi.org/10.1111/ecog.04271.
Preston, F. W. 1962. “The Canonical Distribution of Commonness and Rarity: Part I.” Ecology 43 (2): 185. https://doi.org/10.2307/1931976.